Littlewood-Paley heuristic for derivative

Quick description

The effect of a derivative on a function f is to accentuate the high frequencies and diminish the low frequencies.

Prerequisites

Fourier transform

Example 1

Suppose that we want to study the rate of change of a typical 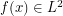$f(x)\in L^{2}$ that is not differentiable eg. $=|x|1_{[-1,1]}(x)$ , or not even weakly differentiable eg. Weierstrass function.

General discussion

The Littlewood–Paley theory states that one can decompose a function 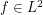$f\in L^{2}$ (and even Schwartz space) as

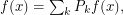
$f(x)=\sum_{k}P_{k}f(x),$

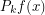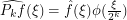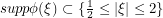where the blocks $P_{k}f(x)$ are localized in Fourier space on the kth dyadic annulus i.e. $\widehat{P_{k}f}(\xi)=\hat{f}(\xi)\phi(\frac{\xi}{2^{k}})$ with $supp\phi(\xi)\subset \{\frac{1}{2}\leq |\xi|\leq 2 \}$ . One can show that for $p\in [1,\infty]$ we have

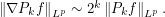
$\left \| \nabla P_{k}f \right \|_{L^{p}}\sim 2^{k}\left \| P_{k}f \right \|_{L^{p}}.$

So we have the heuristic relationship 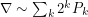$\nabla \sim \sum_{k}2^{k}P_{k}$ .

1427 reads
Subscribe

Comments

Post new comment

(Note: commenting is not possible on this snapshot.)