Quick description
In some situations the existence of a limit can be derived by using inferior or superior limit and suitably dividing a domain to use self-similarity.
Prerequisites
Basic real analysis.
Example 1: Maximal density of a packing
Fix a compact domain 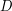 in Euclidean space
in Euclidean space 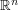 (for example, a ball). A packing
(for example, a ball). A packing 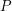 is then a union of domains congruents to
is then a union of domains congruents to 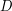 , with disjoint interiors. The density of a packing is defined as
, with disjoint interiors. The density of a packing is defined as
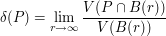
where 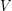 is the volume and
is the volume and 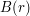 is the square
is the square ![[-r,r]^n](../images/tex/8d62954f58a0b0ac8094b9244c1c9160.png) , when the limit exists.
, when the limit exists.
The present trick shows that if 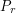 is a packing contained in
is a packing contained in 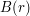 of maximal volume, then
of maximal volume, then 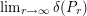 exists.
exists.
First, since ![\delta(P_r)\in [0,1]](../images/tex/aa3ca310bda9528c49dceb2139a4a959.png) , the superior limit
, the superior limit
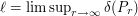 exists. We want to prove that the inferior limit equals the superior one. Given any
exists. We want to prove that the inferior limit equals the superior one. Given any 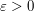 , there is an
, there is an 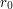 such that
such that 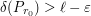 . Now for any integer
. Now for any integer 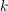 the square
the square 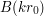 can be divided into
can be divided into 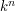 translates of
translates of 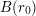 . Each of these contains a packing of density greater than
. Each of these contains a packing of density greater than 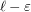 , so that
, so that 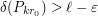 for all
for all 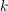 . This rewrites as
. This rewrites as 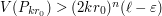 . By maximality,
. By maximality, 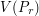 is non-decreasing in
is non-decreasing in  ; for all
; for all 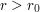 one can introduce
one can introduce 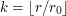 and gets
and gets 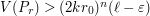 . It follows that
. It follows that
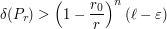
so that as soon as  is large enough,
is large enough, 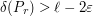 . As a consequence,
. As a consequence, 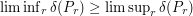 and we are done.
and we are done.
Example 2: Weyl's inequality and polynomial equidistribution
This example is taken from a mathoverflow question and answer.
Let 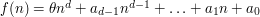 be a polynomial with real coefficients, and
be a polynomial with real coefficients, and 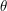 irrational. Let
irrational. Let
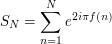
Weyl's Equidistribution theorem for polynomials is equivalent to the claim that 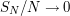 as
as 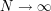 . Though it is not the most easy way to prove this, let us deduce this theorem from the following Weyl's inequality.
. Though it is not the most easy way to prove this, let us deduce this theorem from the following Weyl's inequality.
Let 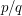 be a rational number in lowest terms with
be a rational number in lowest terms with 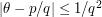 . Weyl's Inequality is the bound:
. Weyl's Inequality is the bound:
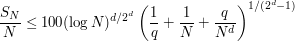
If 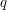 and
and 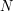 are both large enough, and of the same order of magnitude, then the right-hand side gets small. The point is that the conditions on
are both large enough, and of the same order of magnitude, then the right-hand side gets small. The point is that the conditions on 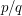 prevent one to apply this to arbitrary
prevent one to apply this to arbitrary 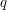 . However, Dirichlet's theorem tells us that arbitrary high
. However, Dirichlet's theorem tells us that arbitrary high 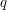 satisfy the needed condition, so that Weyl's inequality implies
satisfy the needed condition, so that Weyl's inequality implies 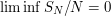 .
.
Now the trick comes into play: the right-hand side in Weyl's inequality does not depend on  , but only on
, but only on 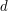 . It therefore gives a uniform bound simultaneously for the sum
. It therefore gives a uniform bound simultaneously for the sum 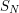 and the sums
and the sums 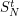 computed using
computed using 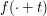 instead of
instead of  .
.
For all  , there is therefore a
, there is therefore a 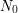 such that for all
such that for all 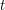 ,
, 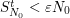 . Then given any
. Then given any 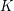 , one has
, one has
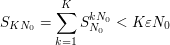
Then, for all 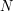 , letting
, letting 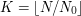 we get that
we get that 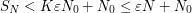 . It follows that
. It follows that 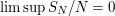 .
.
General discussion
The principle of the trick is the following: dividing the domain (either geometric in optimization setting, of the domain of sumation or integration) can allow you to take an estimate on your sequence that holds at a point, and propagate it to all its multiples. Then, for all other terms you usually get a bounded additional error term, which is hopefully negligible. This can especially be applied when a compactness argument provides you with an inferior or superior limit.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)