Quick description
If one wants to show "If A, then B", first find an interesting consequence C of B that looks easier to prove than B itself, but not so simple that it can be immediately deduced from A. Then try to prove "If A, then C". Finally, show "If A and C, then B". The point is that this factors the original problem into two simpler ones. If one believes that the original implication is true, then the two sub-implications must be true also, so one is not "losing" anything by trying this method.
A variant approach, once one has successfully obtained "If A, then C", is to deconstruct that proof in order to find out what made it work; this can then give valuable clues as to how to then prove the stronger statement "If A, then B". This tends to work well when C acts as a "simplified toy model" of B.
Prerequisites
Example 1
For instance, if trying to prove an identity of the form 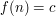 , where
, where 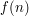 is some expression depending on a parameter
is some expression depending on a parameter  , and
, and  is independent of
is independent of  , one might first try to establish the simpler statement "
, one might first try to establish the simpler statement "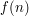 is independent of
is independent of  ", and then to establish
", and then to establish 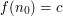 for some special value
for some special value 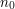 of
of  (note that
(note that 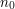 could be an asymptotic value, such as infinity).
could be an asymptotic value, such as infinity).
Note that many proofs of identities by induction are basically of this form.
General discussion
This post is based on this Google Buzz article by Terence Tao.
 Tricki
Tricki
Comments
Independent
Mon, 06/09/2010 - 09:38 — tiptapProving the consequence first is a great way to simplify a problem.
But I don't understand the example. What exactly does "independent" mean. How can f(n) be independent of n?
Sorry if this is a stupid question, but I would really like to understand this.
is independent of if the
Thu, 09/09/2010 - 22:05 — taoEquivalently,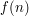 is independent of
is independent of  if one has
if one has 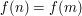 for all
for all 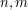 .
.
Thank you
Sun, 12/09/2010 - 21:10 — tiptapThat's a great explanation. Thanks.
Post new comment
(Note: commenting is not possible on this snapshot.)