 Tricki
TrickiDonkey_2009
Personal information
- Name
- Donkey-Tooth Ausundannayan
- About you
Time for some \TeX:
\documentclass[10pt,oneside,a4paper]{article} \usepackage[english]{babel} \usepackage{textcomp} \usepackage{tikz} \usetikzlibrary{arrows} \addtolength{\oddsidemargin}{-.875in} \addtolength{\evensidemargin}{-.875in} \addtolength{\textwidth}{1.75in} \addtolength{\topmargin}{-.875in} \addtolength{\textheight}{1.875in} \begin{document} \begin{center} PROBLEMS OF VECTOR ANALYSIS\\ {\bf BY MURRAY R SPIEGEL}\\ \end{center} Chapter 1 — {\bf VECTORS and SCALARS} \begin{enumerate} \item State which of the following are scalars and which are vectors. \begin{tabbing} (a) weight
 \= (c) specific heat
\= (c) specific heat \= (e) density
\= (e) density \= (g) volume
\= (g) volume \= (i) speed \\
(b) calorie \> (d) momentum \> (f) energy \> (h) distance \> (j) magnetic field intensity \\
\end{tabbing}
\item \begin{tabbing} Represent graphically \= (a) a force of 10N in a direction 30 \textdegree{} north of east \\
\>(b) a force of 15N in a direction 30 \textdegree{} east of north. \\ \end{tabbing}
\item An automobile travels 3km due north, then 5km northeast. Represent these displacements graphically and determine the resultant displacement (a) graphically, (b) analytically.
\item Find the sum or resultant of the following displacements:\\
\= (i) speed \\
(b) calorie \> (d) momentum \> (f) energy \> (h) distance \> (j) magnetic field intensity \\
\end{tabbing}
\item \begin{tabbing} Represent graphically \= (a) a force of 10N in a direction 30 \textdegree{} north of east \\
\>(b) a force of 15N in a direction 30 \textdegree{} east of north. \\ \end{tabbing}
\item An automobile travels 3km due north, then 5km northeast. Represent these displacements graphically and determine the resultant displacement (a) graphically, (b) analytically.
\item Find the sum or resultant of the following displacements:\\
 , 10m northwest;
, 10m northwest;  , 20m 30 \textdegree{} north of east;
, 20m 30 \textdegree{} north of east; 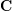 , 35m due south.
\item Show that addition of vectors is commutative, i.e
, 35m due south.
\item Show that addition of vectors is commutative, i.e 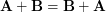 .
\item Show that addition of vectors is associative, i.e.
.
\item Show that addition of vectors is associative, i.e.  .
\item Forces
.
\item Forces 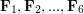 act as shown on an object
act as shown on an object  . What force is needed to prevent
. What force is needed to prevent 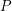 from moving?
\begin{center}
\begin{tikzpicture}[scale=0.4]
\draw [arrows={latex'-latex'}] (2.5,5) – (5,5) – (5,2.5);
\draw [arrows={latex'-latex'}] (0,10) – (5,5) – (11,1);
\draw [arrows={latex'-latex'}] (8,7) – (5,5) – (9,10);
\node at (7.0,5.6) {\small
from moving?
\begin{center}
\begin{tikzpicture}[scale=0.4]
\draw [arrows={latex'-latex'}] (2.5,5) – (5,5) – (5,2.5);
\draw [arrows={latex'-latex'}] (0,10) – (5,5) – (11,1);
\draw [arrows={latex'-latex'}] (8,7) – (5,5) – (9,10);
\node at (7.0,5.6) {\small 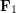 };
\node at (8.0,2.5) {\small
};
\node at (8.0,2.5) {\small 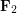 };
\node at (5.55,3.7) {\small
};
\node at (5.55,3.7) {\small 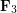 };
\node at (3.8,4.5) {\small
};
\node at (3.8,4.5) {\small 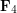 };
\node at (2.0,7.0) {\small
};
\node at (2.0,7.0) {\small 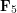 };
\node at (6.5,8.0) {\small
};
\node at (6.5,8.0) {\small 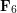 };
\node at (5.0,5.8) {\small
};
\node at (5.0,5.8) {\small  };
\end{tikzpicture}
\end{center}
\item Given vectors
};
\end{tikzpicture}
\end{center}
\item Given vectors  ,
,  and
and 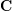 , construct (a)
, construct (a) 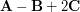 (b)
(b) 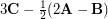 .
\begin{center}
\begin{tikzpicture}[scale=0.25]
\draw [arrows={-latex'}] (0,2) – (6,8);
\draw [arrows={-latex'}] (3.8,3.1) – (11,0);
\draw [arrows={-latex'}] (12,8.5) – (14.0,2.5);
\node at (2.5,5.5) {\small
.
\begin{center}
\begin{tikzpicture}[scale=0.25]
\draw [arrows={-latex'}] (0,2) – (6,8);
\draw [arrows={-latex'}] (3.8,3.1) – (11,0);
\draw [arrows={-latex'}] (12,8.5) – (14.0,2.5);
\node at (2.5,5.5) {\small  };
\node at (13.6,6.4) {\small
};
\node at (13.6,6.4) {\small  };
\node at (6.9,1.0) {\small
};
\node at (6.9,1.0) {\small 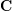 };
\end{tikzpicture}
\end{center}
\item An aeroplane moves in a northwesterly direction at 125km/h relative to the ground, owing to the fact that there is a westerly wind of 50km/h relative to the ground. How quickly and in what direction would the plane have travelled if there were no wind?
\item Given two non-collinear vectors
};
\end{tikzpicture}
\end{center}
\item An aeroplane moves in a northwesterly direction at 125km/h relative to the ground, owing to the fact that there is a westerly wind of 50km/h relative to the ground. How quickly and in what direction would the plane have travelled if there were no wind?
\item Given two non-collinear vectors 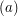 and
and 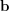 , find an expression for any vector
, find an expression for any vector  lying in the plane determined by
lying in the plane determined by 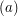 and
and 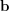 .
\item Given three non-coplanar vectors
.
\item Given three non-coplanar vectors 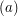 ,
, 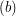 and
and  , find an expression for any vector
, find an expression for any vector  in three dimensional space.
\item Prove that if
in three dimensional space.
\item Prove that if  and
and 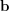 are non-collinear then
are non-collinear then 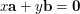 implies
implies 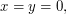 \item Prove that if
\item Prove that if 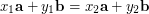 , where
, where  and
and 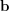 are non-collinear, then
are non-collinear, then 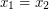 and
and 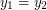 .
\item Prove that if
.
\item Prove that if  ,
, 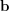 and
and  are non-coplanar then
are non-coplanar then 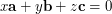 implies
implies 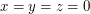 .
\item Prove that if
.
\item Prove that if 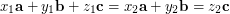 , where
, where  ,
,  and
and  are non-collinear, then
are non-collinear, then 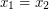 ,
, 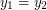 and
and 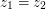 .
\item Prove that the diagonals of a parallelogram bisect one another.
\item If the midpoints of the consecutive sides of any quadrilateral are connected by straight lines, prove that the resulting quadrilateral is a parallelogram.
\item Let
.
\item Prove that the diagonals of a parallelogram bisect one another.
\item If the midpoints of the consecutive sides of any quadrilateral are connected by straight lines, prove that the resulting quadrilateral is a parallelogram.
\item Let  ,
, 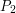 and
and 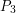 be points fixed relative to an origin
be points fixed relative to an origin 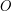 and let
and let  ,
, 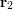 and
and 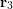 be position vectors from
be position vectors from 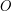 to each point. Show that if the vector equation
to each point. Show that if the vector equation 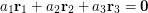 holds with respect to origin
holds with respect to origin 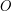 then it will hold with respect to any other origin
then it will hold with respect to any other origin 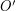 if and only if
if and only if 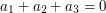 .
\item Find the equation of a straight line which passes through two given points
.
\item Find the equation of a straight line which passes through two given points 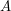 and
and 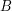 having position vectors
having position vectors  and
and 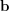 with respect to an origin
with respect to an origin 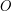 .
\item (a) Find the position vectors
.
\item (a) Find the position vectors  and
and 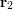 for the points
for the points 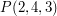 and
and 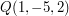 of a rectangular co-ordinate system in terms of the unit vectors
of a rectangular co-ordinate system in terms of the unit vectors 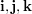 . (b) Determine graphically and analytically the resultant of these position vectors.
\item Prove that the magnitude
. (b) Determine graphically and analytically the resultant of these position vectors.
\item Prove that the magnitude 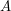 of the vector
of the vector 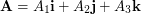 is
is 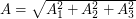 .
\item Given
.
\item Given 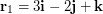 ,
, 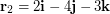 ,
, 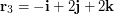 , find the magnitudes of (a)
, find the magnitudes of (a) 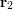 , (b)
, (b) 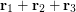 , (c)
, (c) 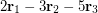 .
\item If
.
\item If 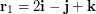 ,
, 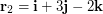 ,
, 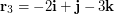 and
and 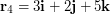 , find scalars
, find scalars 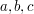 such that
such that 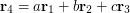 .
\item Find a unit vector parallel to the resultant of vectors
.
\item Find a unit vector parallel to the resultant of vectors 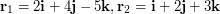 .
\item Determine the vector having initial point
.
\item Determine the vector having initial point  and terminal point
and terminal point 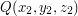 and find its magnitude.
\item Forces
and find its magnitude.
\item Forces  ,
,  and
and 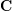 acting on an object are given in terms of their components by the vector equations
acting on an object are given in terms of their components by the vector equations 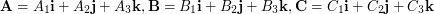 . Find the magnitude of the resultant of these forces.
\item Determine the angles
. Find the magnitude of the resultant of these forces.
\item Determine the angles  ,
,  and
and 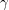 which the vector
which the vector 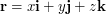 makes with the positive directions of the coordinate axes and show that \begin{center}
makes with the positive directions of the coordinate axes and show that \begin{center} 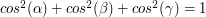 . \\ \end{center}
(The numbers
. \\ \end{center}
(The numbers 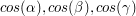 are called the \emph{direction cosines} of the vector
are called the \emph{direction cosines} of the vector  .)
\item Determine a set of equations for the straight line passing through the points
.)
\item Determine a set of equations for the straight line passing through the points 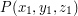 and
and 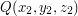 .
\item Given the scalar field defined by
.
\item Given the scalar field defined by 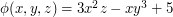 find
find 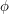 at the points \\ (a)
at the points \\ (a) 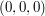 , (b)
, (b)  , (c)
, (c) 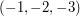 .
\item Graph the vector fields defined by: \\ (a)
.
\item Graph the vector fields defined by: \\ (a) 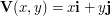 , (b)
, (b) 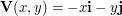 , (c)
, (c) 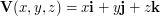 .
\end{enumerate}
\end{document}
.
\end{enumerate}
\end{document}
History
- Member for
- 8 years 39 weeks