Quick description
If  is an idempotent in a ring
is an idempotent in a ring  (not necessarily with identity), then we can decompose
(not necessarily with identity), then we can decompose  as the direct sum of four components (subrings), each of them related to
as the direct sum of four components (subrings), each of them related to  . Concretely,
. Concretely,
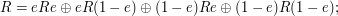
note that here 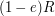 is just notation that means
is just notation that means 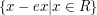 ,
and similarly for
,
and similarly for 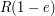 .
.
This decomposition is known as the Peirce decomposition of  with respect to
with respect to  .
.
An important feature of this decomposition is that each of
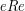 and
and 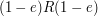 is a subring of
is a subring of  , and the former even
has an identity, namely, the element
, and the former even
has an identity, namely, the element  , which does indeed lie
in
, which does indeed lie
in 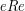 , since
, since 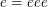 ; also,
; also, 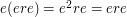 for all
for all 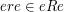 .
.
If  does contain an identity
does contain an identity  , then
, then 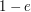 is defined,
and is again an idempotent, and one has
is defined,
and is again an idempotent, and one has 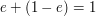 (obviously),
and
(obviously),
and 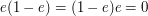 since
since 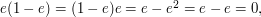 as
as  is idempotent. One says that
is idempotent. One says that  and
and 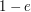 form a pair
of orthogonal idempotents.
Furthermore, in this case, the subring
form a pair
of orthogonal idempotents.
Furthermore, in this case, the subring 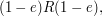 as defined above,
coincides with the set of products
as defined above,
coincides with the set of products 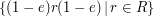 .
(A similar remark applies to each of
.
(A similar remark applies to each of 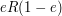 and
and 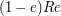 .)
.)
More generally, continuing to assume that  contains an identity,
if
contains an identity,
if 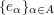 is a set of orthogonal idempotents for
is a set of orthogonal idempotents for  with the property that
with the property that 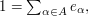 then
then
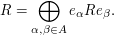
Prerequisites
The basic idea of decomposing a ring via idempotents should be accessible to anyone knowing the basics of ring theory. Several of the examples below refer to contexts which require a more specialized degree of knowledge; in such cases, this is indicated at the beginning of the example.
Example 1
If  lies in the centre of
lies in the centre of  (in particular,
if
(in particular,
if  is commutative), then
is commutative), then 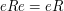 ,
,
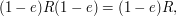 and
and 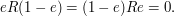 Thus we obtain
the simpler decomposition
Thus we obtain
the simpler decomposition 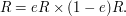
Example 2
This example requires
a basic knowledge of the costruction of the spectrum
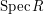 of a commutative ring
of a commutative ring  with identity.
with identity.
If  is commutative with
is commutative with  and
and 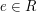 is an idempotent, then
is an idempotent, then
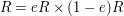 , as noted in Example 1. As remarked above,
we may form the idempotent
, as noted in Example 1. As remarked above,
we may form the idempotent 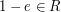 , and so
in particular, both
, and so
in particular, both 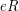 and
and 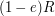 are commutative rings with identity (namely
are commutative rings with identity (namely
 and
and 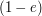 respectively).
Thus
respectively).
Thus 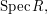
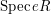 , and
, and 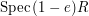 are all defined, and the factorization
are all defined, and the factorization 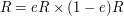 induces a
decomposition
induces a
decomposition
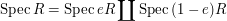
of 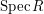 into a union of two open subsets. Conversely,
any such decomposition of
into a union of two open subsets. Conversely,
any such decomposition of 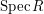 arises from an idempotent
arises from an idempotent 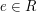 in this way.
in this way.
In short, if we think of  as being the ring of
regular functions on
as being the ring of
regular functions on 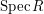 ,
then idempotents in
,
then idempotents in  serve precisely as the
indicator (or characteristic) functions of simultaneously
open and closed
subsets of
serve precisely as the
indicator (or characteristic) functions of simultaneously
open and closed
subsets of 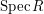 . (In particular,
. (In particular, 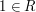 is the indicator
function of
is the indicator
function of 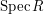 itself, while
itself, while 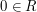 is the indicator function
of
the empty subset.)
is the indicator function
of
the empty subset.)
Note that in the case that  is a Boolean ring,
so that every element is idempotent (by definition), the space
is a Boolean ring,
so that every element is idempotent (by definition), the space
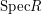 is totally disconnected, and the above discussion
specializes to the
Stone representation theorem.
is totally disconnected, and the above discussion
specializes to the
Stone representation theorem.
Example 3
This example requires some familiarity with topological group theory, including the notion of Haar measure on a locally compact topological group, and various related notions.
Suppose that  is a topological group which admits a
neighbourhood basis of
the identity consisting of compact open subgroups. (A basic example of such a group is
is a topological group which admits a
neighbourhood basis of
the identity consisting of compact open subgroups. (A basic example of such a group is 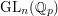 , the general linear group of invertible
, the general linear group of invertible 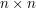 -matrices over the field
-matrices over the field 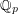 of
of  -adic numbers.)
One consequence of this assumption is that
-adic numbers.)
One consequence of this assumption is that  is locally compact, and so we can choose a Haar measure
is locally compact, and so we can choose a Haar measure 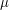 on
on  .
.
Let 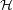 denote the
denote the 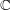 -vector space of all compactly supported
locally constant
-vector space of all compactly supported
locally constant 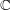 -valued functions on
-valued functions on  . We can make
. We can make 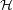 into
a
into
a 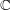 -algebra by defining a convolution product on its elements as follows:
-algebra by defining a convolution product on its elements as follows:
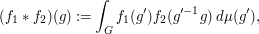
for any two functions 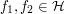 .
The
.
The 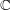 -algebra
-algebra 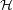 is then referred to as the
Hecke algebraof the group
is then referred to as the
Hecke algebraof the group  .
.
If 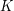 is any compact open subgroup of
is any compact open subgroup of  , then we may define an idempotent
, then we may define an idempotent
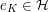 via the formula
via the formula 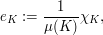 where
where 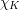 is the
indicator (or characteristic) function of
is the
indicator (or characteristic) function of 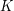 .
Since
.
Since 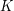 is open, the function
is open, the function 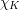 is
locally constant and compactly supported, and thus
lies in
is
locally constant and compactly supported, and thus
lies in 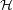 , and hence so does
, and hence so does 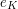 .
.
In this situation, for any 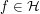 , the convolution
, the convolution
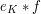 is the function obtained by averaging
is the function obtained by averaging  on the
left via the action of the compact open subgroup
on the
left via the action of the compact open subgroup 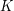 , and simililarly
, and simililarly
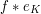 is the is the function obtained by averaging
is the is the function obtained by averaging  via the action of
via the action of
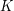 on the right.
In particular
on the right.
In particular
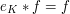 if and only
if
if and only
if 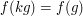 for all
for all 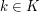 and
and 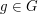 , and simililarly,
, and simililarly,
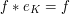 if and only if
if and only if 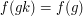 for all
for all 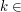 K and
K and 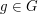 .
Thus the subalgebra
.
Thus the subalgebra 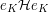 of
of 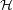 consists of those elements of
consists of those elements of 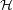 that are bi-invariant under
the action of
that are bi-invariant under
the action of 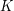 , i.e. such that
, i.e. such that 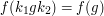 for all
for all
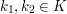 and
and 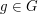 .
.
Since any 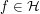 is compactly supported and locally constant,
by virtue of our assumption on
is compactly supported and locally constant,
by virtue of our assumption on  we may find some sufficiently small
compact open subgroup
we may find some sufficiently small
compact open subgroup 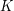 such that
such that  is bi-
is bi-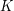 -invariant. Thus
we find that
-invariant. Thus
we find that
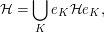
where the union is indexed by the collection of all compact open subgroups of  .
.
 Tricki
Tricki
Comments
Change of title, and other matters
Sat, 25/04/2009 - 04:24 — emertonI propose changing the title of this article to ``How to exploit idempotents in a ring''.
I have used this idea many times in my research, but never knew it was called the Peirce decomposition until reading this article. Indeed, it is a standard example in the theory of schemes, and in the representation theory of p-adic groups, which motivate two of the above examples, but I have never seen it referred to by this name in any books on those subjects. (I say this just as a defense in advance of my ignorance of this name; I don't think I will be unique in having an interest in this article, while not knowing the name ``Peirce decomposition".)
If there are no objections within a day or so, I will make this change. I will then add a line to the quick description along the lines of ``this decomposition is sometimes refereed to as the Peirce decomposition of with respect to
with respect to  ''.
''.
Also, the ``More generally'' remark about a complete system of orthogonal idempotents should be elaborated on. (Because if does not have an identity, then
does not have an identity, then 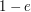 is not actually defined as an element of
is not actually defined as an element of  , and so the Peirce decomposition is itself more general than decomposing with respect to orthogonal idempotents. So while the decomposition by a complete system of orthogonal idempotents is very closely related to the Peirce decomposition, it does not always contains the latter as a special case. Indeed, the notion of a complete system of orthogonal idempotents probalby only makes sense if
, and so the Peirce decomposition is itself more general than decomposing with respect to orthogonal idempotents. So while the decomposition by a complete system of orthogonal idempotents is very closely related to the Peirce decomposition, it does not always contains the latter as a special case. Indeed, the notion of a complete system of orthogonal idempotents probalby only makes sense if  has an identity, at least as far as I can tell.)
has an identity, at least as far as I can tell.)
Finally, I noticed that the earlier version of this article was to some extent lifted from PlanetMath. Maybe we should be careful doing this in general, just for copyright reasons.
I've discussed titles quite a
Sat, 25/04/2009 - 10:07 — gowersI've discussed titles quite a bit in this forum post. If you buy my view about imperative titles, then you could consider "Exploit idempotents in a ring." But it depends whether the point of the article is more "You might not have thought of it, but idempotents are actually very useful," or "You have seen or heard that idempotents can be useful, but here is how to produce such arguments for yourself." If the former, then I would be very much in favour of the imperative title. Or one could go for something more specific, such as "Decompose your ring using idempotents." The ideal, in my view is a title that serves as a super-quick summary of the message of the entire article. It's not always possible to achieve that, but often it is.
Title explanation
Sat, 25/04/2009 - 10:37 — JoseBroxI agree mostly with you in this issue - Imperative and how-to titles are desirable. That's why I created stubs for "How to work without an identity element when you clearly need it", etc.
But my main purpose creating this article was not to explain how to use idempotents (for that, I created the other articles). My main purpose was to help those people that has heard about Peirce decomposition but does not see anything special about it.
The main example I have in mind (I'm new to the field, so there's not that much I can think of!)is when you want to prove a categorical statement about a ring without identity (mostly about R-Mod), and typical "universal" or homological techniques with pretty diagrams do not seem to work; then your "other option" is to switch to ring decompositions like Peirce's (or, in a sort of generalization of this, to exploit some Morita context if you have it).
without identity (mostly about R-Mod), and typical "universal" or homological techniques with pretty diagrams do not seem to work; then your "other option" is to switch to ring decompositions like Peirce's (or, in a sort of generalization of this, to exploit some Morita context if you have it).
Based on Tim's suggestion,
Sat, 25/04/2009 - 14:59 — emertonBased on Tim's suggestion, let me second his proposal of ``Decompose your ring using idempotents''.
``Peirce decomposition'' may be standard in some ring theory circles, but it is not at all standard among algebraic geometers/commutative algebraists, nor among representation-theorists, both of whom would be interested in this article. As I said, I had never before heard of it (the name, that is, not the concept), and I have been studying these fields for close to fifteen years. I'm not saying this to pull rank, but rather to point out that this name is not nearly as well-known as the concept, and so there will be many people interested in the contents of this page who wouldn't have any idea about its contents under the present name.
As a possible compromise,
Sat, 25/04/2009 - 17:09 — gowersAs a possible compromise, what about a link to this article on the "How to use" page, called "How to use the Peirce decomposition"? The title of the article would be different, but there's no problem with that. There could be a hidden-text quick description that said that the Peirce decomposition was a decomposition of rings using idempotents.
That sounds sensible. I
Sun, 26/04/2009 - 03:57 — emertonThat sounds sensible. I don't object at all to using the phrase Peirce decomposition to describe this procedure, as long as we don't rely on it as the only means of navigating to this page. I think in general that it is better to avoid using names (especially people's names) for things if one can avoid it, unless the name is absolutely universally known or absolutely unavoidable.
Thus ``Prove that your holomorphic function is bounded" (or some variant of this) would be better than ``Apply Liouville's theorem" as an instruction related to trying to show that a holomorphic functions is constant. After all, there is always the possibility that someone doesn't know or has forgotten what Liouville's theorem says, and then the name carries absolutely no hint about the method. (As a contrast, ``Apply the maximum modulus theorem'' is probably not quite as bad in this respect, because it contains in its name at least some semblance of what it is about.)
Not sure about title change
Sat, 25/04/2009 - 10:21 — JoseBroxThanks a lot for the editions!
As far as I can tell (that is, very little!), the name "Peirce decomposition" is standard in ring theory (which is my area of expertise, but I've been on it just for six months now!). I can't be sure about changing the title to something more general about idempotents, because there are other, related but different (if I'm not mistaken!), ways of using idempotents. For example, we say that a ring (not necessarily with unity)has enough idempotents if there exists a subset
(not necessarily with unity)has enough idempotents if there exists a subset 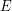 of orthogonal idempotents (
of orthogonal idempotents (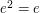 ,
, 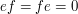 ), so that we can decompose
), so that we can decompose  as a direct sum of the principal right ideals
as a direct sum of the principal right ideals 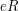 (equivalently
(equivalently 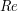 ). Note that
). Note that 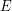 must be infinite in order to be interesting. I wanted to write different articles for these two concepts (and one more general, titled "How to work without an identity element when you clearly need it" introducing also sets of local units, firm rings, etc).
must be infinite in order to be interesting. I wanted to write different articles for these two concepts (and one more general, titled "How to work without an identity element when you clearly need it" introducing also sets of local units, firm rings, etc).
I agree that the "more general" statement is not right just now: indeed, we must ask for to have identity and also the set should be finite (I wrote it late and I somewhat messed the idea up with the enough idempotents thing!).
to have identity and also the set should be finite (I wrote it late and I somewhat messed the idea up with the enough idempotents thing!).
Actually, I didn't lift anything of PlanetMath! I just made a quick summary on my own. I checked now with PlanetMath, there is an obvious resemblance because it is a definition but I don't see that much of a coincidence!
Dear Jose, Sorry for the
Sat, 25/04/2009 - 14:54 — emertonDear Jose,
Sorry for the unfair PlanetMath comment; indeed, it must just be that there are not all that many ways to describe the basics of this concept.
Best wishes,
Matthew
Post new comment
(Note: commenting is not possible on this snapshot.)