Quick description
Functional analysis is the study of infinite-dimensional vector spaces. Typically these are spaces of functions such as 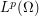 being the space of functions
being the space of functions  where
where
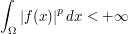
for 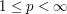 .
These spaces must have a topology, which is often given in terms of a norm such as
.
These spaces must have a topology, which is often given in terms of a norm such as
![\|f\|_{L^p} = \left[\int_\Omega |f(x)|^p \, dx\right]^{1/p}.](../images/tex/ca7d06d85917917a3674a6eddb893c51.png)
The name comes from the notion of functionals which are continuous linear functions 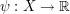 where
where  is the space concerned. A major early problem was the identification of ways of representing the functionals of a given infinite dimensional space
is the space concerned. A major early problem was the identification of ways of representing the functionals of a given infinite dimensional space  . For example, the Riesz representation theorem (or perhaps one should say theorems) says that if
. For example, the Riesz representation theorem (or perhaps one should say theorems) says that if ![C[a,b]](../images/tex/d930e3053f32dbc51f14e870df59674d.png) is the space of continuous functions
is the space of continuous functions ![[a,b]\to\R](../images/tex/ac03d8bb716633cfff9572518186b4d3.png) , then any functional
, then any functional ![C[a,b]\to\R](../images/tex/f528da26b7f7e4035c4bf326f555c3d9.png) , with the norm
, with the norm 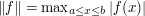 on
on ![C[a,b]](../images/tex/d930e3053f32dbc51f14e870df59674d.png) , could be represented in terms of a function
, could be represented in terms of a function  of bounded variation with
of bounded variation with
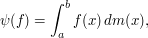
where the integral is understood in the Riemann-Stieltjes sense. Related results concern, for example, the functionals on 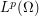 spaces.
spaces.
Such analysis quickly led to the classification of infinite-dimensional spaces: Banach spaces, Hilbert spaces, reflexive spaces, and investigation of their properties.
This is a large area and involves large parts of classical and modern analysis. It is used in a large number of subjects, but especially partial differential equations, geometric analysis, quantum mechanics, and dynamical systems, to give a small sample of relatively applied parts of mathematics that use functional analysis.
Prerequisites
Calculus, basic analysis.
General discussion
Here is a (small) sample of topics:
-
representation of functionals
-
dual spaces, topologies
-
different notions of convergence: strong, weak, weak*
-
topological vector spaces
-
operator algebras
-
spaces of (linear) operators
-
geometry of Banach spaces
-
spaces of measures with values in (Banach) spaces (see vector measure)
-
existence of solutions to operator equations: solve
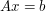 for
for 
-
fixed point and minimax theorems
-
Fredholm operators and Fredholm index
-
compactness of sets in specific spaces
-
optimization of functions defined on spaces (see Convex and variational analysis)
-
differential equations on spaces and evolution equations
-
convex and variational analysis
-
particular (classes of) spaces: e.g., Sobolev spaces, Orlicz spaces,
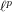 ,
, 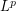 ,
, 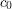
 Tricki
Tricki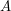
Comments
Expand section...
Sat, 19/06/2010 - 12:23 — UlagatinHi,
First of all, an excellent site! It's great to have such a compendium of mathematical knowledge online, accessable to all. So a great deal of thanks goes to the creators of this site!
I'm in Year 12 in Australia and I just stumbled upon this page [on functional analysis], and I'd love to see it expanded. It looks to be an interesting field! I assume that capital Omega here is a space/topology, maybe even a set being integrated over? Could an explanation be given of the theory behind L^p(Omega) spaces and how it ties in more broadly to this topic?
I look forward to hearing further (and just as a side-note, I believe my mathematical background to be good so far - I have a good understanding of convergence of sequences, Maclaurin series, complex numbers, derivatives of inverse trigonometric functions, etc). I have read a little of analysis, to which I have been impressed so far, but that I have only broadly skimmed.
Thanks once again.
Davin
Post new comment
(Note: commenting is not possible on this snapshot.)