 |
Quick description
To understand the standard Hölder inequality better it is helpful to look at a more general version and use a geometric picture of convex bodies.
Prerequisites
Undergraduate analysis.
Example 1
Say, we want to bound the integral
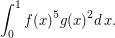
Our current knowledge allows us to estimate the integrals
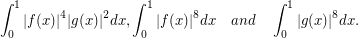
How can we see quickly, whether this information is sufficient or not? Secondly, how are we going to choose the coefficients in Hoelder's inequality?
This type of problem is common in analytic number theory, for example.
General discussion
Hölder's inequality states that on any measure space 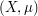 , and any measurable
, and any measurable 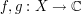 , one has
, one has
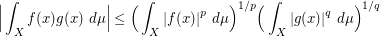
whenever we have 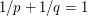 .
.
The key insight here is to view this as an statement about interpolation to get information at the point 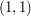 from information at the points
from information at the points 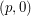 and
and 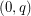 . The condition
. The condition 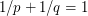 ensures that all three points lie on a line.
ensures that all three points lie on a line.
Once we have this realisation, it is easy to generalise this to the case of the example above. To obtain information at the point 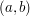 , as in the integral
, as in the integral
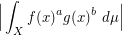
it is sufficient to have bounds at three points 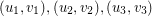 such that
such that 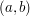 lies in the convex hull of the three points.
lies in the convex hull of the three points.
The coefficients in the estimate are then given by the coefficients of the convex linear combination of 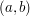 inside the triangle
inside the triangle 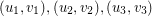 .
.
The simplicity of the geometric view allows us to handle more complex integrals integrals like
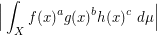
with the same ease.
By drawing the corresponding points in the plane, it is easy to judge in advance which of the integrals contributes most to the estimate later, thus providing a tool to estimate the quality of the estimate.
 Tricki
Tricki
Comments
Article classification
Wed, 15/10/2014 - 16:09 — lukeI am not quite sure where to put this article. There is a 'use convexity' link in the 'estimating integrals' section but also one for Hölder's inequality.
I guess the best would be a link from both articles (if they exist one day) to this one?
Post new comment
(Note: commenting is not possible on this snapshot.)