How to determine whether a finitely presented group is finite

Quick description

There is no general algorithm that will determine whether a given finitely presented group is finite or not. However, there are a number of strategies to try.

Prerequisites

Basic definitions of combinatorial group theory.

General discussion

This article could use additional contributions. I have another idea or two to add, but other strategies would be greatly appreciated!

Suppose that $G$ is a finitely presented group. It is easy to find quotients of $G$ ; adding relations to the presentation and determining the consequences amounts to passing to a quotient of $G$ by the normal closure of the relations. Then if you can add relations to $G$ and end up with a group that you know to be infinite, it follows that the original group was infinite.

Example 1

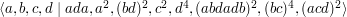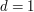Let $G$ be the finitely presented group with presentation $\langle a, b, c, d \mid ada, a^2, (bd)^2, c^2, d^4, (abdadb)^2, (bc)^4, (acd)^2 \rangle$ . Trying to determine explicitly whether there are infinitely many reduced words in $G$ seems hopelessly complicated. Instead, let's notice that if we add the relation $d = 1$ , then this group collapses to 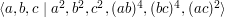$\langle a, b, c \mid a^2, b^2, c^2, (ab)^4, (bc)^4, (ac)^2 \rangle$ , which we recognize as the infinite Coxeter group $[4,4]$ .

4356 reads
Subscribe

Comments

methods to show that a group is infinite

Tue, 09/06/2009 - 17:32 — Danny Calegari (not verified)

I have a couple of posts on my blog (http://lamington.wordpress.com) with lots of examples of ways to show that a group is finite/infinite, probably too many/too specialized for the tricki. You are welcome to mine these posts for anything you think is relevant.

Post new comment

(Note: commenting is not possible on this snapshot.)