Quick description
Compactness is an all-pervasive concept in mathematics. But it is also a tool that can be used for solving problems. This article briefly explains some typical uses (see the quick descriptions) and gives links to other more detailed articles.
The articles
Convergent subsequences and diagonalization Quick description ( A topological space is sequentially compact if every sequence has a convergent subsequence. One form of the Bolzano-Weierstrass theorem states that a closed bounded subset of 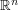 is sequentially compact. More generally, compact metric spaces are sequentially compact. These facts have many applications. Also, some useful diagonalization techniques can be interpreted as saying that certain topological spaces are sequentially compact – as a result, one often hears the phrase "by compactness" when no topology has been specifically mentioned. )
is sequentially compact. More generally, compact metric spaces are sequentially compact. These facts have many applications. Also, some useful diagonalization techniques can be interpreted as saying that certain topological spaces are sequentially compact – as a result, one often hears the phrase "by compactness" when no topology has been specifically mentioned. )
Discretization followed by compactness arguments Quick description ( Often one proves a theorem about a continuous structure by finding a fairly dense finite subset of it and proving a finite statement about that instead. For this one needs the continuous structure to have a suitable compactness property. )
Using the fact that a continuous function on a compact set attains its bounds Quick description ( A continuous real-valued function defined on a compact topological space is bounded and attains its bounds. This fact has many applications, as this article demonstrates with some varied examples. )
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)