Quick description
This article provides a list of different ways to study groups by their actions.
General discussion
Click here for a brief discussion of group actions. ( Many groups arise naturally as groups of transformations of one kind or another. For example, the cyclic group of order  can be thought of as the group of rotations of a regular
can be thought of as the group of rotations of a regular  -gon. But even a group that arises in a different way can often be thought of very fruitfully as a group of transformations: it's just that one has to find a mathematical object to be transformed.
-gon. But even a group that arises in a different way can often be thought of very fruitfully as a group of transformations: it's just that one has to find a mathematical object to be transformed.
More formally, if  is a group, and
is a group, and  is a set, then an action of
is a set, then an action of  on
on  is a homomorphism
is a homomorphism 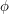 from
from  to the set
to the set 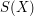 of all bijections from
of all bijections from  to
to 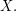 That is, for each
That is, for each 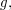
 is a bijection from
is a bijection from  to
to 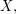 and these bijections need to compose in a way that reflects the multiplication in
and these bijections need to compose in a way that reflects the multiplication in 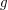 : we need
: we need  to be
to be 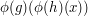 for every
for every 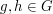 and every
and every 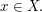 If we are dealing with just one action, it can be nicer to write
If we are dealing with just one action, it can be nicer to write  instead of
instead of 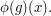 That is, we think of
That is, we think of 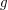 as actually equalling a bijection rather than being transformed into one. Then the rule is that
as actually equalling a bijection rather than being transformed into one. Then the rule is that 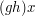 should equal
should equal 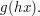 (This is actually the definition of a left action. Analogously, we can write
(This is actually the definition of a left action. Analogously, we can write 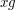 for
for 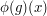 , in which case we require that
, in which case we require that 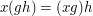 . This is the definition of a right action.) Note that using the word "homomorphism" rather than "isomorphism" is intentional here: perhaps surprisingly, actions are often very useful even if different elements of
. This is the definition of a right action.) Note that using the word "homomorphism" rather than "isomorphism" is intentional here: perhaps surprisingly, actions are often very useful even if different elements of  have the same effect on
have the same effect on 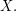
Sometimes the set  is just a finite set, in which case a bijection from
is just a finite set, in which case a bijection from  to
to  is naturally thought of as a permutation, and the action of
is naturally thought of as a permutation, and the action of  as a homomorphism from
as a homomorphism from  to the symmetric group on
to the symmetric group on 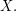 But often
But often  has more structure: it might be a vector space, or a topological space, say. Then the interesting actions are the ones where the bijections from
has more structure: it might be a vector space, or a topological space, say. Then the interesting actions are the ones where the bijections from  to
to  are the structure preserving ones: invertible linear maps in the case of vector spaces, and homeomorphisms in the case of topological spaces. )
are the structure preserving ones: invertible linear maps in the case of vector spaces, and homeomorphisms in the case of topological spaces. )
The articles
-
Proving results by letting a group act on a finite set Quick description ( This article discusses various ways of deducing facts about groups by choosing appropriate actions on finite sets. Sometimes the group itself acts, and sometimes another group acts on a set that is defined in terms of the first group.)
-
To show that a group element is non-trivial, show that it has a non-trivial action or image Quick description ( A group
 may be defined so indirectly that it can be difficult to distinguish one group element from another; but often there are ways to map
may be defined so indirectly that it can be difficult to distinguish one group element from another; but often there are ways to map  to a more concrete group, or to make
to a more concrete group, or to make  act on a more concrete space. Using such concrete representations, it becomes easier to distinguish elements in
act on a more concrete space. Using such concrete representations, it becomes easier to distinguish elements in  .)
.) -
Representation theory Quick description ( When the set
 on which a group acts is a vector space and the bijections are linear, we have what is called a representation of the group. Representations are a very powerful way of studying groups. They also have many other applications, and representation theory is regarded as a branch of mathematics in its own right.)
on which a group acts is a vector space and the bijections are linear, we have what is called a representation of the group. Representations are a very powerful way of studying groups. They also have many other applications, and representation theory is regarded as a branch of mathematics in its own right.) -
Use topology to study your group Quick description ( If you want to study a group
 , then it can help to realize
, then it can help to realize  as the fundamental group of a topological space. This works best when
as the fundamental group of a topological space. This works best when  is infinite and discrete, and especially if
is infinite and discrete, and especially if  is finitely presented and torsion-free.)
is finitely presented and torsion-free.)
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)