Quick description
An important general principle in probability is that a sum of bounded independent random variables, each of mean 0, has a very small probability of having a large modulus, where "large" means substantially larger than its standard deviation. For example, if you toss a coin 1000 times, then the probability that the number of heads does not lie between 400 and 600 is tiny. This principle can be proved rigorously – see Example 3 of bounding probabilities by expectations. Also, and this is the main theme of this article, the assumption of independence can be weakened in a way that makes the principle much more widely applicable.
Prerequisites
Basic concepts of probability, graph theory, metric spaces.
 |
Example 1
Let 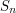 be the symmetric group on
be the symmetric group on  elements. There is a natural graph with
elements. There is a natural graph with 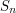 as its vertex set, where two permutations
as its vertex set, where two permutations 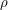 and
and  are joined if and only if
are joined if and only if 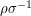 is a transposition, or equivalently
is a transposition, or equivalently 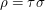 for some transposition
for some transposition 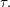 This graph gives us a natural metric on
This graph gives us a natural metric on 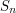 : the distance between two permutations
: the distance between two permutations 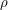 and
and  is the smallest
is the smallest  such that we can find
such that we can find  transpositions
transpositions 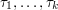 with
with 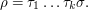
Now let 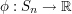 be a function that is 1-Lipschitz with respect to this distance. This is equivalent to the assumption that
be a function that is 1-Lipschitz with respect to this distance. This is equivalent to the assumption that  whenever there is a transposition
whenever there is a transposition  such that
such that 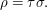 (An obvious example of such a function is the function
(An obvious example of such a function is the function 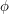 where
where 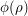 is defined to be the smallest
is defined to be the smallest  such that
such that 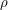 is a product of
is a product of  transpositions.) Since every permutation can be written as a product of at most
transpositions.) Since every permutation can be written as a product of at most 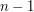 transpositions and an
transpositions and an  -cycle needs exactly
-cycle needs exactly 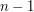 transpositions, the diameter of
transpositions, the diameter of 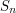 is
is 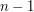 , so
, so 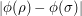 cannot exceed
cannot exceed 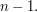 We shall show that
We shall show that 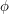 is "highly concentrated", in the sense that for almost all pairs
is "highly concentrated", in the sense that for almost all pairs 
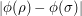 is far smaller than
is far smaller than  – it is rarely much more than
– it is rarely much more than 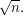
General discussion
Before we get on to the proof, we need to state Azuma's inequality, and before we do that we need to say what a martingale is. The latter is simple. Let 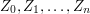 be a sequence of random variables. They are a martingale if for every
be a sequence of random variables. They are a martingale if for every  the expectation of
the expectation of 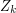 given the values of
given the values of 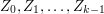 is
is 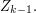
It is perhaps clearer to express this in terms of the martingale difference sequence 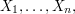 where
where 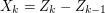 for each
for each  . Then the martingale condition is that the expectation of
. Then the martingale condition is that the expectation of 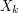 given the values of
given the values of 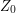 and
and 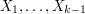 is always
is always 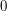 . An obvious example is when the
. An obvious example is when the 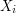 are independent random variables with mean
are independent random variables with mean 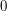 , but as we shall see there is an easy way of generating many more examples than this.
, but as we shall see there is an easy way of generating many more examples than this.
Suppose that each variable 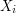 takes values between
takes values between 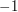 and
and  . Then Azuma's inequality states that the probability that
. Then Azuma's inequality states that the probability that 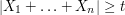 is at most
is at most 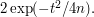 More generally, if
More generally, if 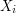 takes values between
takes values between  and
and 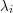 , then the probability that
, then the probability that 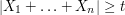 is at most
is at most 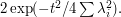
Now let us return to our example, and see how we can define a martingale in a very natural way.
Example 1, continued
Recall that we have a function 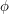 defined on
defined on 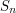 , with the property that if
, with the property that if 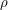 and
and  are partitions such that
are partitions such that 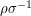 is a transposition, then
is a transposition, then 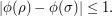 In order to define a martingale difference sequence, we choose a random permutation
In order to define a martingale difference sequence, we choose a random permutation 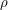 and "reveal information about
and "reveal information about 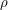 little by little".
little by little".
What does this mean? Well, we look at the values of 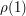 ,
,  ,
,  , and so on, and at the
, and so on, and at the  th stage we define
th stage we define 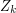 to be the expected value of
to be the expected value of 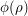 given the values
given the values 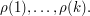 In other words,
In other words, 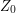 is just
is just 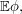
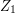 is the expected value of
is the expected value of 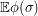 given that
given that 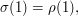 and in general
and in general 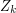 is the expected value of
is the expected value of 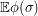 given that
given that 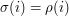 for every
for every 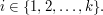
What can we say about 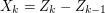 ? We would like to prove an upper bound for the maximum absolute value that
? We would like to prove an upper bound for the maximum absolute value that 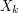 can take, and we would also like to prove that the expectation of
can take, and we would also like to prove that the expectation of 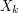 given the values of
given the values of 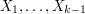 is
is 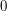 .
.
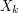 is the amount by which the expectation of
is the amount by which the expectation of 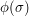 can change if we add to our existing knowledge of the values of
can change if we add to our existing knowledge of the values of 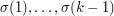 the knowledge that
the knowledge that 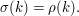 To get an upper bound for this, let us define
To get an upper bound for this, let us define 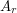 , for each
, for each  not in the set
not in the set 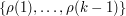 , to be the set of all
, to be the set of all  such that
such that 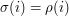 for every
for every 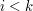 and
and 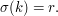 Now let us pick
Now let us pick  and
and 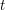 and define a bijection
and define a bijection 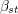 between
between 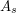 and
and 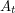 as follows. Given a permutation
as follows. Given a permutation 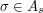 , let
, let 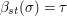 agree with
agree with  except that
except that 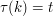 and
and  To put this another way,
To put this another way,  where
where 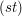 is the transposition that exchanges
is the transposition that exchanges  and
and 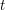 .
.
Now the distance between  and
and 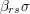 is at most 1 (and exactly 1 if
is at most 1 (and exactly 1 if 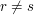 ). Therefore,
). Therefore, 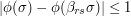 for every
for every 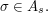 It follows that
It follows that ![\mathbb{E}[\phi(\sigma)|\sigma\in A_s]](../images/tex/8e7dc3c0c08e2ffb3b263241031cc296.png) differs from
differs from ![\mathbb{E}[\phi(\sigma)|\sigma\in A_t]](../images/tex/d9cf17048a5c47b5f2fce8e2cb1475df.png) by at most 1.
by at most 1.
In other words, once we know what 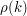 is, the difference it can make to our expectation of
is, the difference it can make to our expectation of 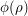 is at most 1. Also, the average of
is at most 1. Also, the average of 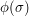 given that
given that 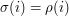 for every
for every 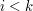 is the average over
is the average over  of the averages of
of the averages of 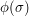 over
over 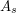 (since all the sets
(since all the sets 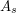 have the same size), so the expectation of
have the same size), so the expectation of 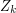 given
given 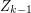 is
is 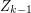 , as we wanted. (Equivalently, the expectation of
, as we wanted. (Equivalently, the expectation of 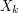 given
given 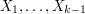 is
is 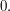 )
)
We have now checked the facts we wanted to check: we have a martingale and the random variables 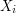 in the martingale difference sequence take values in
in the martingale difference sequence take values in ![[-1,1]](../images/tex/d060b17b29e0dae91a1cac23ea62281a.png) . It follows from Azuma's inequality that the probability that
. It follows from Azuma's inequality that the probability that 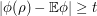 is at most
is at most 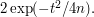 From this we see that even though the diameter of
From this we see that even though the diameter of 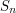 is
is 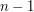 , for the vast majority of pairs
, for the vast majority of pairs  the difference
the difference 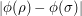 is at most
is at most 
General discussion
The proof of Azuma's inequality is a relatively straightforward generalization of the proof given in Example 3 of bounding probabilities by expectations, which deals with the special case where the martingale difference sequence consists of independent random variables that take values in ![[-1,1].](../images/tex/64cf5e98e343bc8538ef055f8d796112.png)
 Tricki
Tricki
Comments
possible typo?
Fri, 29/05/2009 - 00:38 — alexThe article says
"Then the martingale condition is that the expectation of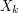 given the values of
given the values of 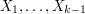 is always 0."
is always 0."
I see that the martingale condition implies this, but is it true that the martingale condition "is" this? This condition can be satisfied without the sequence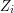 being a martingale.
being a martingale.
Indeed, suppose A, B are independent random variables with mean zero. Define
 . Clearly,
. Clearly, ![E[X_1]=0, E[X_2| X_1]=E[A | B]=0](../images/tex/655c0dab70c4a904ba93deab985c4a70.png) , so the above condition holds. On the other this is not a martingale:
, so the above condition holds. On the other this is not a martingale: ![E[Z_2|Z_1, Z_0] = Z_1 + Z_0](../images/tex/4049ae7b8de3c2354dbb4706859b5080.png) which may not equal
which may not equal 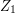 .
.
Thanks – I've corrected
Fri, 29/05/2009 - 21:55 — gowersThanks – I've corrected it. I've tended to deal with martingales, such as the one in this permutations example, where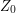 is constant, which is why I wrote what I wrote.
is constant, which is why I wrote what I wrote.
Trivia
Mon, 22/06/2009 - 19:56 — Didier Piau (not verified)There is a typo in the second paragraph of section Example 1, continued: one should cancel the symbol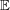 in the two occurrences of
in the two occurrences of
the expected value of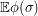 given that
given that
And, reading the last paragraph of this section, I wondered why you picked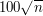 as an example of extremely unlikely deviation. First,
as an example of extremely unlikely deviation. First, 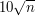 would already yield a rather respectable (i.e., small) bound, namely, something like
would already yield a rather respectable (i.e., small) bound, namely, something like 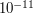 . Second, there is nothing specific about
. Second, there is nothing specific about 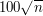 here, although the formulation seems to indicate otherwise: you might want to add a for example somewhere.
here, although the formulation seems to indicate otherwise: you might want to add a for example somewhere.
Thank you for this article.
Post new comment
(Note: commenting is not possible on this snapshot.)