Quick description
One can often draw interesting consequences from the information that a certain random variable is almost constant. In many contexts, a good definition of "is almost constant" is "has small variance". The reason this is a good definition is that of all measures of near constancy, the variance is arguably the most natural and is often the easiest to calculate. This is best illustrated with some examples.
Prerequisites
Two equivalent definitions of variance of a random variable, basic definitions concerning sets, graphs etc.
Example 1
This example may seem slightly artificial, but in fact it is an important argument in additive combinatorics.
Let 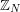 denote the set of integers mod
denote the set of integers mod 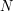 . Let
. Let 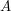 be a subset of
be a subset of 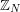 of size
of size 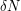 . Define an additive quadruple in
. Define an additive quadruple in 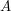 to be a quadruple
to be a quadruple 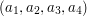 of elements of
of elements of 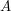 with the property that
with the property that 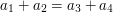 . Suppose that the number of additive quadruples of elements of
. Suppose that the number of additive quadruples of elements of 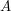 is at most
is at most 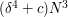 . We shall show, provided
. We shall show, provided  is small enough, that
is small enough, that 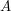 must contain an arithmetic progression of length 3. More precisely, we shall show that there must exist
must contain an arithmetic progression of length 3. More precisely, we shall show that there must exist  and
and 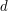 such that neither
such that neither 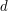 nor
nor 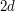 is equal to 0 mod
is equal to 0 mod 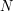 , and
, and  ,
, 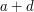 and
and 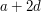 all belong to
all belong to 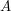 .
.
To do this, we define a function  as follows: for each
as follows: for each 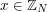 ,
, 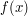 is the number of ways of writing
is the number of ways of writing  as
as 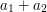 with
with 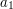 and
and 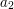 belonging to
belonging to 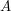 . The following facts about
. The following facts about  are easy to see. First,
are easy to see. First,
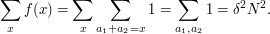
Secondly,
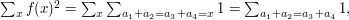
which is the number of additive quadruples of elements of 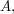 which we are assuming to be at most
which we are assuming to be at most 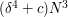 .
.
It follows that the average value of 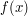 is
is 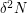 and the average value of
and the average value of 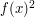 is at most
is at most 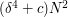 . Therefore, the variance of
. Therefore, the variance of  , which is
, which is 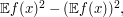 is at most
is at most 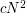 .
.
We now use Chebyshev's inequality, which tells us that if 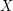 is any random variable, then
is any random variable, then ![\mathbb{P}[|X-\mathbb{E}X|\geq t]\leq\mathrm{Var} X/t^2.](../images/tex/9782e00f12a92e56d673e69f0453ad70.png) Here is a quick proof of the inequality, which is also discussed in the article Bounding probabilities by expectations. We know that
Here is a quick proof of the inequality, which is also discussed in the article Bounding probabilities by expectations. We know that 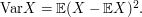 This is certainly at least
This is certainly at least 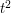 times the probability that
times the probability that 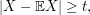 so the inequality follows. For us the random variable is
so the inequality follows. For us the random variable is 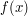 , where
, where  is chosen randomly and uniformly from
is chosen randomly and uniformly from 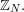 Applying Chebyshev's inequality, we find that the proportion of
Applying Chebyshev's inequality, we find that the proportion of  such that
such that 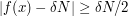 is at most
is at most 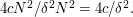 Therefore, if
Therefore, if  the number of
the number of  such that
such that 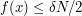 is at most
is at most 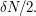
Now 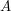 has
has 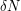 elements, so there must be at least
elements, so there must be at least 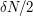 elements
elements 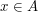 such that
such that 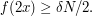 This implies that the number of triples
This implies that the number of triples 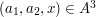 such that
such that 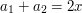 is at least
is at least 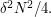 Each such triple corresponds to an arithmetic progression
Each such triple corresponds to an arithmetic progression 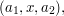 as long as
as long as 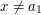 and
and 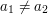 . The number of these degenerate triples is at most
. The number of these degenerate triples is at most 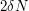 , so as long as
, so as long as 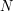 is sufficiently large (it is enough if
is sufficiently large (it is enough if 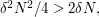 which is the case if
which is the case if 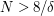 ) there must be non-degenerate ones, as claimed.
) there must be non-degenerate ones, as claimed.
General discussion
Let us think briefly about how the above argument might have been discovered. The idea was to find some fairly general condition on a set 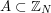 that would guarantee that
that would guarantee that 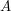 contained an arithmetic progression of length 3. Now
contained an arithmetic progression of length 3. Now 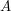 will certainly contain an arithmetic progression of length 3 if we can find some
will certainly contain an arithmetic progression of length 3 if we can find some 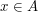 such that
such that 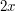 can be written in many ways as
can be written in many ways as 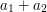 , with
, with 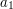 and
and 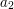 also belonging to
also belonging to 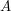 . And this will certainly be the case if the function
. And this will certainly be the case if the function  defined above is close to its average value
defined above is close to its average value  for more than
for more than 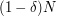 values of
values of  . Speaking more loosely, we would like
. Speaking more loosely, we would like  to be roughly constant. So it is natural to look at the variance of
to be roughly constant. So it is natural to look at the variance of  , which turns out to be closely related to the number of additive quadruples in the set
, which turns out to be closely related to the number of additive quadruples in the set 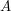 .
.
 |
 Tricki
Tricki
Comments
I may be dense
Wed, 15/06/2011 - 08:29 — kodlu.. but I can't understand why "the proportion of x such that | f(x) - delta N | \geq (delta N / 2)" has delta N instead of delta^2 N which is the average value of f(x) as stated previously. And I haven't been able to turn inline commenting on in google chrome, my apologies.
Post new comment
(Note: commenting is not possible on this snapshot.)