Quick description
Suppose that you are given a real number, to many significant figures, told that it is close to a rational with small denominator, and asked to find that rational. Can this be done efficiently (where "efficient" means that you can identify the rational 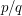 in a time that depends polynomially on the number of digits of
in a time that depends polynomially on the number of digits of 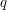 )? Yes it can, with the help of continued fractions.
)? Yes it can, with the help of continued fractions.
Prerequisites
Elementary number theory, continued fractions.
Example 1
Suppose you are told that the number 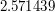 is very close to a fraction
is very close to a fraction 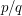 such that
such that 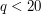 . How can you find this fraction? For numbers this small, trial and error would work fine. (For each
. How can you find this fraction? For numbers this small, trial and error would work fine. (For each 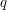 less than
less than 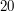 , one could find the
, one could find the 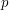 that makes
that makes 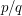 closest to
closest to 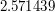 and wait until you hit it almost exactly.) But for larger numbers, trial and error would take a hopelessly long time.
and wait until you hit it almost exactly.) But for larger numbers, trial and error would take a hopelessly long time.
There is a simple method for solving this computational problem. First, let us imagine that the number in question actually equals 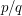 . Then we can express
. Then we can express 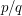 as a continued fraction, which takes a time that is at worst proportional to the number of digits of
as a continued fraction, which takes a time that is at worst proportional to the number of digits of 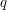 (assuming that
(assuming that 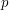 and
and 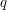 are of roughly comparable size). For example, if the number were
are of roughly comparable size). For example, if the number were 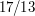 (but we didn't know that) then we would write it as
(but we didn't know that) then we would write it as 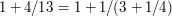 . But then we note that if our number is merely very close to
. But then we note that if our number is merely very close to 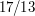 , then we will write it as
, then we will write it as 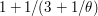 , where
, where 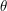 is very close to
is very close to  . At that point, we recognise that we are very close to the rational
. At that point, we recognise that we are very close to the rational 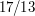 .
.
In our example, we see that
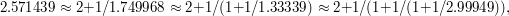
at which point we recognise that the original fraction was very close to 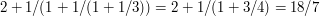 .
.
General discussion
This method plays an important role in Shor's quantum algorithm for factorizing, since the procedure outputs a real number that is close to a rational and one needs an efficient way of finding the denominator of that rational.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)