 |
Quick description
You are given a (bad) continuous real function  on a compact metric space
on a compact metric space 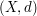 ; suppose you have a tool that applies well for Lipschitz functions, with good monotonicity properties; Then compare
; suppose you have a tool that applies well for Lipschitz functions, with good monotonicity properties; Then compare  with Lipschitz dominators:
For
with Lipschitz dominators:
For 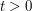 let
let 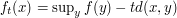 . Then
. Then 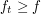 is the minimum Lipschitz dominator for
is the minimum Lipschitz dominator for  with Lipschitz constant
with Lipschitz constant 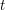 .
.
General discussion
This is a lot like convolution with an approximate delta function; making the translations
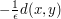 behaves a lot like the delta-function approximation
behaves a lot like the delta-function approximation 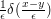 .
.
 Tricki
Tricki
Comments
This looks nice, but do you
Thu, 11/06/2009 - 10:57 — Anonymous (not verified)This looks nice, but do you plan to give some examples of problems where this trick is useful? It would be a big help.
useful!?
Thu, 11/06/2009 - 19:50 — mckeown_j.cOh yes... "tricks" wiki... yeah, it came up in a complex/harmonic analysis course I was taking, but the context... remains elusive.
Closely related is P
Sat, 13/06/2009 - 17:23 — mckeown_j.cClosely related is Péron's expression solving the harmonic Dirichlet problem, as an infimum of sup-harmonic dominators.
Post new comment
(Note: commenting is not possible on this snapshot.)