 |
Quick description
Suppose one wants to find the parameter 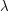 that minimizes a quantity
that minimizes a quantity 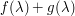 , where
, where  is an increasing non-negative function in
is an increasing non-negative function in 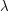 and
and 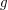 is a decreasing non-negative function in
is a decreasing non-negative function in 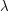 . One can of course use calculus methods to do this, by finding the value(s) of
. One can of course use calculus methods to do this, by finding the value(s) of 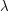 where the derivative of
where the derivative of 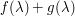 vanishes. But a quick and dirty way to find the minimum approximately is just find the value
vanishes. But a quick and dirty way to find the minimum approximately is just find the value 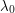 where the two functions agree:
where the two functions agree:
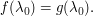
Indeed, since 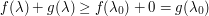 for
for 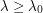 , and
, and 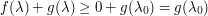 for
for 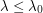 , we see that the minimal value of
, we see that the minimal value of 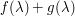 lies between
lies between 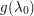 and
and 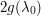 .
.
More generally, once one finds a 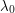 where
where 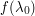 and
and 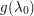 are comparable in magnitude, this is already enough to compute the minimum of
are comparable in magnitude, this is already enough to compute the minimum of 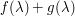 up to multiplicative constants.
up to multiplicative constants.
Prerequisites
Calculus
Example 1
(Optimize expressions such as 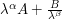 )
)
General discussion
When optimizing a sum 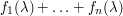 , where the intermediate
, where the intermediate 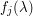 are somehow "in between"
are somehow "in between" 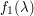 and
and 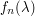 , the above heuristic is often effective (up to a factor of
, the above heuristic is often effective (up to a factor of  , perhaps) if one looks for the
, perhaps) if one looks for the 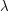 which balances the two extreme terms
which balances the two extreme terms 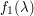 and
and 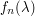 . (Need an example of this...)
. (Need an example of this...)
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)