Quick description
If  and
and 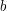 are both coprime to
are both coprime to  , then so is
, then so is 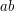 . From this it follows easily that the integers mod
. From this it follows easily that the integers mod  that are coprime to
that are coprime to  form a group under multiplication. This fact leads to simple proofs of several results in elementary number theory.
form a group under multiplication. This fact leads to simple proofs of several results in elementary number theory.
Prerequisites
Basic definitions of modular arithmetic and group theory. Lagrange's theorem.
Example 1: Fermat's little theorem
Let  be a prime. Then every integer that is not a multiple of
be a prime. Then every integer that is not a multiple of  is coprime to
is coprime to  , so the non-zero integers mod
, so the non-zero integers mod  form a group. This group has
form a group. This group has 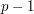 elements, so by Lagrange's theorem every element of the group has order dividing
elements, so by Lagrange's theorem every element of the group has order dividing 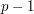 . Therefore,
. Therefore, 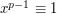 mod
mod  for every integer
for every integer  that is not a multiple of
that is not a multiple of  . This is Fermat's little theorem.
. This is Fermat's little theorem.
Example 2: Euler's theorem
Let  be any positive integer greater than 1. Then the integers coprime to
be any positive integer greater than 1. Then the integers coprime to  form a group under multiplication, and this group has order
form a group under multiplication, and this group has order 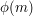 , where
, where 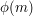 is the number of positive integers less than
is the number of positive integers less than  and coprime to
and coprime to  . By Lagrange's theorem, every element of this group has order dividing
. By Lagrange's theorem, every element of this group has order dividing 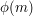 , which implies that
, which implies that 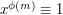 mod
mod  for every integer
for every integer  that is coprime to
that is coprime to  . This is Euler's theorem.
. This is Euler's theorem.
Example 3: Wilson's theorem
What is 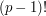 mod
mod  ? Since every
? Since every  between
between  and
and 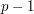 has a multiplicative inverse, we have a lot of cancellation in the product
has a multiplicative inverse, we have a lot of cancellation in the product 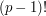 . Indeed, if we take the numbers from
. Indeed, if we take the numbers from  to
to 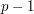 and partition them into sets of the form
and partition them into sets of the form 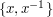 , then it looks as though everything cancels and we get 1. However, this isn't quite right because the set
, then it looks as though everything cancels and we get 1. However, this isn't quite right because the set 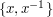 is a singleton if
is a singleton if 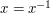 . But this happens only if
. But this happens only if 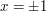 , since if
, since if 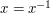 then
then 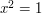 , which implies that
, which implies that 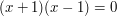 . So everything cancels except for the singleton
. So everything cancels except for the singleton 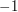 , and we obtain the result that
, and we obtain the result that 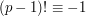 mod
mod  . This is Wilson's theorem.
. This is Wilson's theorem.
The same argument shows that the product of all the positive integers less than  and coprime to
and coprime to  is congruent to
is congruent to 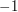 mod
mod  . This observation does not have a name.
. This observation does not have a name.
Example 4: another proof of Euler's (and hence Fermat's) theorem
Let  be a group and let
be a group and let 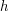 be an arbitrary element of
be an arbitrary element of  . Then the map
. Then the map 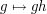 is a bijection from
is a bijection from  to
to  . Proof: the map
. Proof: the map 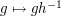 is its inverse. Let
is its inverse. Let  be the group of all integers mod
be the group of all integers mod  that are coprime to
that are coprime to  . Let us list these integers as
. Let us list these integers as 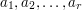 , where
, where 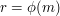 . Let
. Let  be one of them.
be one of them.
Since multiplication by  is a bijection, the product
is a bijection, the product 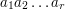 is congruent to the product
is congruent to the product 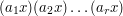 , which is congruent to
, which is congruent to 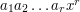 . Multiplying both sides by the inverse of
. Multiplying both sides by the inverse of 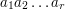 (we happen to know that this is
(we happen to know that this is 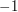 but we do not need to use this fact) we find that
but we do not need to use this fact) we find that 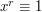 , so Euler's theorem has a group-theoretic proof that does not even use Lagrange's theorem.
, so Euler's theorem has a group-theoretic proof that does not even use Lagrange's theorem.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)