Quick description
Many results about arithmetic modulo a prime  that might seem hard follow naturally and easily from the (non-obvious) fact that the group of non-zero integers mod
that might seem hard follow naturally and easily from the (non-obvious) fact that the group of non-zero integers mod  under multiplication is cyclic.
under multiplication is cyclic.
Prerequisites
This article is aimed at somebody who is meeting modular arithmetic and elementary number theory for the first time. The basic definitions and results are assumed, as is the definition of a cyclic group.
General discussion
Let  be a prime number. Then integers mod
be a prime number. Then integers mod  can be added and multiplied. Under addition, the integers mod
can be added and multiplied. Under addition, the integers mod  form a cyclic group, since they are all generated by the number
form a cyclic group, since they are all generated by the number  . If
. If  is a prime, in which case it is more usual to call it
is a prime, in which case it is more usual to call it  , then the non-zero integers mod
, then the non-zero integers mod  form a group under multiplication as well: this is a much less obvious fact. The group axioms are easy to check, with the exception of the axiom that every element has an inverse. To see why this is the case, note that if
form a group under multiplication as well: this is a much less obvious fact. The group axioms are easy to check, with the exception of the axiom that every element has an inverse. To see why this is the case, note that if  is prime and
is prime and  is not a multiple of
is not a multiple of  , then
, then 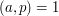 , so there exist integers
, so there exist integers 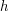 and
and  such that
such that 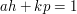 , which tells us that
, which tells us that 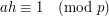 . Thus,
. Thus, 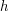 is a multiplicative inverse for
is a multiplicative inverse for  .
.
The theme of this article is that the non-zero integers mod  do not just form a group: they form a cyclic group. Moreover, the fact that they form a cyclic group is a fact that can be used. It is the latter that makes this topic appropriate for a Tricki article: however, the proof that the group is cyclic itself uses several beautiful and generalizable techniques, so we include it in an appendix.
do not just form a group: they form a cyclic group. Moreover, the fact that they form a cyclic group is a fact that can be used. It is the latter that makes this topic appropriate for a Tricki article: however, the proof that the group is cyclic itself uses several beautiful and generalizable techniques, so we include it in an appendix.
One final remark: the results we prove here can also be proved without using the fact that the multiplicative group mod  is cyclic. Since it takes a little work to prove that it is cyclic, there is a case for preferring the more elementary arguments. The merit of using the fact that the multiplicative group is cyclic is not that it gives the best proof of any individual result. But once you know that it is cyclic, a number of results follow very easily, so this approach has the effect of unifying a number of disparate facts and making their proofs seem less ad hoc.
is cyclic. Since it takes a little work to prove that it is cyclic, there is a case for preferring the more elementary arguments. The merit of using the fact that the multiplicative group is cyclic is not that it gives the best proof of any individual result. But once you know that it is cyclic, a number of results follow very easily, so this approach has the effect of unifying a number of disparate facts and making their proofs seem less ad hoc.
Example 1: The multiplicativity of the Legendre symbol and Euler's criterion
A non-zero integer  mod
mod  is called a quadratic residue if there is some
is called a quadratic residue if there is some 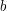 such that
such that 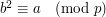 . The Legendre symbol
. The Legendre symbol 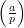 is defined to be
is defined to be  if
if  is a quadratic residue and
is a quadratic residue and 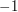 if
if  is a quadratic non-residue.
is a quadratic non-residue.
An important fact about the Legendre symbol is that it is multiplicative: that is, 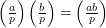 . Another well-known result is Euler's criterion, which states that
. Another well-known result is Euler's criterion, which states that 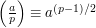 . Let us see why both these results are obvious if the multiplicative group mod
. Let us see why both these results are obvious if the multiplicative group mod  is cyclic (which it is).
is cyclic (which it is).
To say that the multiplicative group is cyclic is to say that there is a generator. In other words, there exists a non-zero integer  such that every integer mod
such that every integer mod  is congruent to some power of
is congruent to some power of  . This implies that the non-zero integers mod
. This implies that the non-zero integers mod  are
are 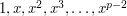 , since if any two of these were the same then there would be fewer than
, since if any two of these were the same then there would be fewer than 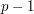 distinct powers of
distinct powers of  and
and  would not be a generator. Furthermore,
would not be a generator. Furthermore, 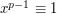 , either by Fermat's little theorem, or by the observation that
, either by Fermat's little theorem, or by the observation that 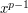 cannot be congruent to
cannot be congruent to 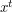 for some
for some 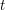 between 1 and
between 1 and 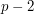 without
without 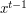 being congruent to
being congruent to 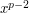 , which we have argued is not the case.
, which we have argued is not the case.
Looked at from this perspective, the quadratic residues mod  are just the even powers of
are just the even powers of  . Why? Well, let
. Why? Well, let  be a quadratic residue. We know that we can write
be a quadratic residue. We know that we can write  as
as 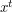 for some
for some 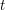 between
between 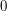 and
and 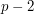 . If
. If  is a quadratic residue, then there exists
is a quadratic residue, then there exists 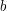 such that
such that 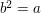 , and
, and 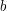 can be written as
can be written as 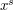 with
with  between
between 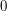 and
and 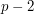 . Therefore,
. Therefore, 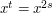 . If
. If 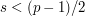 , then this proves that
, then this proves that 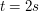 , so
, so 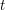 is even. If
is even. If 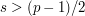 , then
, then 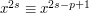 , so
, so 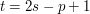 , which is again even. (To put this more neatly, one might say that the quadratic residues are the numbers of the form
, which is again even. (To put this more neatly, one might say that the quadratic residues are the numbers of the form 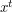 where
where 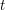 is a multiple of
is a multiple of 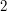 in the additive group mod
in the additive group mod 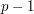 . But since
. But since 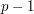 is even, the least residue of such a
is even, the least residue of such a 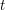 must be even.) Conversely, if
must be even.) Conversely, if 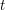 is even, then
is even, then 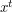 is obviously a quadratic residue, since it is the square of
is obviously a quadratic residue, since it is the square of 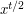 . This proves that there are precisely
. This proves that there are precisely 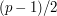 quadratic residues.
quadratic residues.
Why is the Legendre symbol multiplicative? Because the above reasoning shows that 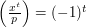 .
.
Why does Euler's criterion hold? Well, 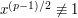 but
but 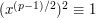 ,
and the roots of
,
and the roots of 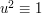 are
are 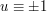 , so
, so 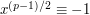 . And then we see that
. And then we see that 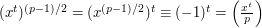 .
.
General discussion
What we are doing is looking at the integers mod  on a "logarithmic scale". We take what is known as the discrete logarithm (base
on a "logarithmic scale". We take what is known as the discrete logarithm (base  ), and difficult-looking multiplicative facts turn into easy-looking additive facts.
), and difficult-looking multiplicative facts turn into easy-looking additive facts.
Example 2: The number of cubes mod 
How many cubic residues are there mod  ? The answer turns out to be that if
? The answer turns out to be that if 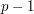 is a multiple of
is a multiple of 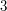 then there are
then there are 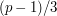 of them, and otherwise there are
of them, and otherwise there are 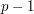 .
.
To see this, let  be a generator of the multiplicative group. The cubic residues are all numbers of the form
be a generator of the multiplicative group. The cubic residues are all numbers of the form 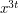 for some integer
for some integer 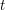 . So how many of these are there that are distinct mod
. So how many of these are there that are distinct mod  ? To answer that, let us answer the following question: for which values of
? To answer that, let us answer the following question: for which values of  is it possible to find
is it possible to find 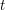 such that
such that 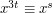 ?
?
To answer this question, we note that 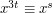 if and only if
if and only if 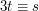 mod
mod 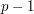 . If
. If 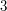 is not a factor of
is not a factor of 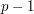 then
then 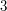 is invertible mod
is invertible mod 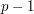 so the congruence
so the congruence 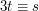 mod
mod 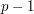 is soluble for every
is soluble for every  . Therefore, there are
. Therefore, there are 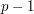 cubic residues. If
cubic residues. If 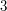 is a factor of
is a factor of 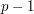 , then the distinct multiples of 3 mod
, then the distinct multiples of 3 mod 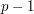 are
are 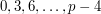 , of which there are
, of which there are 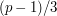 . And the result is proved.
. And the result is proved.
Appendix
Not yet written.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)