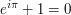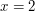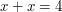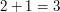See also the formatting of sections page.
You can experiment with markup and other features of the Tricki in the Sandbox.
| What it looks like | What you type | ||||
|---|---|---|---|---|---|
[maths euler|Euler's identity] e^{i \pi} + 1 = 0[/maths] |
|||||
 can be factorised as can be factorised as 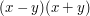 . . |
$x^2 - y^2$ can be factorised as $(x-y)(x+y)$. |
||||
Some shortcuts: 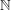 , , 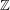 , , 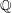 , , 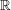 , , 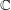 . . |
Some shortcuts: $\N$, $\Z$, $\Q$, $\R$, $\C$. |
||||
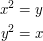
|
[maths]\begin{align} |
||||
| Link to Tricki article How to use Zorn's lemma. | [[How to use Zorn's lemma]] |
||||
| Link to the same article. | [[How to use Zorn's lemma|same article]] |
||||
| Blending: we do not have many Dummy articles. | [[Dummy article]]s |
||||
| Link to a non-article page on the Tricki. | Link to a [[forum/|non-article page on the Tricki]]. |
||||
| Link to Wikipedia article on mathematics. | Link to [[w:Mathematics|Wikipedia article on mathematics]]. |
||||
| Link to preprint on the arXiv. | Link to [[arxiv:math/0408230|preprint on the arXiv]]. |
||||
| Link to review on MathSciNet. | Link to [[mathscinet:16335|review on MathSciNet]]. |
||||
| Link to Google search. | Link to [[google:Mathematics|Google search]]. |
||||
| External link to the Prime Pages. | External link to [http://primes.utm.edu/ the Prime Pages]. |
||||
 |
[image sierpinski.gif|Sierpinski triangle] |
||||
|
[image sierpinski.gif|left|Sierpinski triangle] |
||||
| Reference to (Euler's identity) above. | Reference to [eqref euler] above. |
||||
[theorem ftba|Fundamental theorem of basic arithmetic]Let $x = 2$. Then $x + x = 4$.[/theorem] |
|||||
| Note: always use descriptive IDs and not position dependent ones in order to make restructuring articles earier. | |||||
Proof of Theorem 1. This is obvious.□
|
[proof ftba]This is obvious.[/proof] |
||||
By Theorem 1, 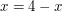 . . |
By [ref Theorem #ftba], $x = 4 - x$. |
||||
Example 1
This is an example section; see the formatting sections page for more information.
|
[EXAMPLE extag] This is an example section; see the [[tricki/help/formatting-structure|formatting sections]] page for more information.[/EXAMPLE] |
||||
| Here is a reference to Example 1. | Here is a [ref reference to Example #extag]. |
||||
| You can make bits of text bold, italic or even both. | You can make bits of text '''bold''', ''italic'' or '''''even both'''''. |
||||
|
|
||||
|
|
||||
Heading 1Heading 2 |
|
||||
| Link to heading 1 above. | [[#Heading 1|Link to heading 1]] above. |
||||
| Some hidden text here. (You've found the hidden text!) | [cut]Some hidden text here.||You've found the hidden text![/cut] |
||||
| The proof is obvious. Indeed, 2 + 2 = 4. | [add]The proof is obvious.{{ Indeed, 2 + 2 = 4.}}[/add] |
||||
[frame][lemma important|The Important Lemma] $2 + 1 = 3$ [/lemma][/frame] |
|||||
| Yőü can ûse TeX-stylè acceñts. | Y\H{o}\"u can \^use TeX-styl\`e acce\~nts. |
||||
| You can also use TeX-style dashes — Birch–Swinnerton-Dyer conjecture. | You can also use TeX-style dashes --- Birch--Swinnerton-Dyer conjecture. |
||||
|
<table border="1">
|
||||
| See, for example, the W3Schools page on tables for more information and examples. | |||||
Editorial notes:
|
[note article incomplete]This article is missing large parts of what is required of a Tricki article. |
||||
| Notes can be specified at the article level and the section level. They can be one of three types: 'incomplete', 'contributions wanted', or 'attention'. See the page about editorial markup for more information. | |||||
Available theorem-like environments:
theorem (numbering: theorem)
lemma (numbering: theorem)
corollary (numbering: theorem)
conjecture (numbering: theorem)
proposition (numbering: theorem)
sublemma (numbering: theorem)
problem (numbering: problem)
exercise (numbering: problem)
question (numbering: problem)
definition (numbering: definition)
claim (no numbering)
remark (no numbering)
remarks (no numbering)
The theorem-type environments are rendered in italics; the others are not.
Lists can be nested to an arbitrary depth by putting more asterisks at the beginning of the line.
There are three levels of headings (from === to =====).
Images can also be floated to the right (right instead of left) or centred (centre).
 Tricki
Tricki