 |
Quick description
If you are asked to prove that a mathematical object  has a property
has a property 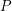 , you will often obtain a clearer and easier problem if you identify certain properties
, you will often obtain a clearer and easier problem if you identify certain properties 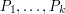 of
of  and then prove the statement "Every object that has properties
and then prove the statement "Every object that has properties 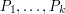 has property
has property 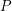 " instead of the original statement "
" instead of the original statement " has property
has property 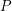 ."
."
 Tricki
Tricki
Comments
Exact functors
Sun, 26/04/2009 - 19:09 — Zygmund (not verified)As an example, how about proving that a functor that preserves exactness in sequences of the form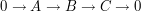 necessarily preserves exactness in sequences of the form
necessarily preserves exactness in sequences of the form 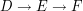 ? One could then apply this to tensor products with a flat module.
? One could then apply this to tensor products with a flat module.
Similar articles?
Mon, 27/04/2009 - 11:34 — JungleBased on the quick descriptions of this article, and the following article:
/article/Think_axiomatically_even_about_concrete_objects
It seems to me that they are getting toward a similar point. Of course both articles are still stubs; if the intention is to explain different tricks, perhaps someone could explain in the quick descriptions how they are different. Just my two cents.
I had noticed that too, and
Mon, 27/04/2009 - 12:46 — gowersI had noticed that too, and considered merging them. I may yet do so, but I want to wait until I have thought of good examples for each. Somehow, with this article the focus is on generalization via abstraction, and thereby obtaining a question that gets more to the heart of the problem, whereas with the other one you may not be generalizing at all, because you may be using an abstract description that completely characterizes the original concrete object. (As an example of the latter, it is very useful to think of the reals as a complete ordered field rather than say as a set of Dedekind cuts, even though there is only one complete ordered field. And it is sometimes helpful to think of the exponential function just as "a" function that satisfies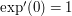 and
and 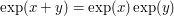 .)
.)
If we do end up with two articles, there's no doubt that they will be closely related, and that this should be highlighted.
Post new comment
(Note: commenting is not possible on this snapshot.)