Quick description
One might think that generalizing a problem would make it harder to solve. However, the reverse is often true. The articles linked to from here explain why.
General discussion
Clarify your problem by making it more abstract Quick description ( If you are asked to prove that a mathematical object 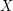 has a property
has a property 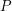 , you will often obtain a clearer and easier problem if you identify certain properties
, you will often obtain a clearer and easier problem if you identify certain properties 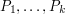 of
of 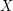 and then prove the statement "Every object that has properties
and then prove the statement "Every object that has properties 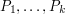 has property
has property 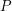 " instead of the original statement "
" instead of the original statement "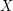 has property
has property 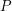 ." See also Think axiomatically even about concrete objects. )
." See also Think axiomatically even about concrete objects. )
Strengthen your inductive hypothesis Quick description ( Suppose that you are trying to prove by induction that a statement 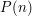 is true for every
is true for every  . If it is hard to deduce
. If it is hard to deduce 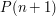 from
from 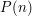 then you may be able to deal with the difficulty by finding a different statement
then you may be able to deal with the difficulty by finding a different statement 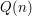 that implies
that implies 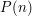 , and deducing
, and deducing 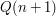 from
from 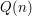 instead (and, of course, proving
instead (and, of course, proving 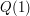 ). )
). )
To understand an object, consider treating it as one of a family of objects and analysing the family Quick description ( An insight that has shaped much of modern mathematics is that it is often better to look at families of mathematical objects rather than at individual objects in isolation. If the family itself has a structure (usually geometric or algebraic) then it may be that this can be exploited: to prove a fact about one of the objects 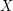 in the family it may be easier to prove a result about all the objects in the family and deduce from it what you want to know about
in the family it may be easier to prove a result about all the objects in the family and deduce from it what you want to know about 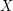 .)
.)
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)