Quick description
Many proofs in many areas of mathematics, but especially in parts of number theory and combinatorics, give rise to bounds that have logarithmic terms. This article is about why that should be, and gives some examples of proofs where they arise. So far it has just one example. It would be good to have many more, demonstrating many different reasons for the appearance of log factors.
Example 1
An aligned rectangle is a rectangle in 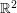 with its sides parallel to the
with its sides parallel to the  and
and 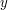 axes. Suppose you have a collection of
axes. Suppose you have a collection of  aligned rectangles. What is the maximum value of
aligned rectangles. What is the maximum value of  for which it is always possible to find either
for which it is always possible to find either  disjoint rectangles in the collection or a point in
disjoint rectangles in the collection or a point in 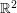 that is contained in
that is contained in  rectangles from the collection? For convenience we shall assume throughout the discussion that all rectangles are closed.
rectangles from the collection? For convenience we shall assume throughout the discussion that all rectangles are closed.
A simple example shows that  cannot be greater than
cannot be greater than 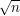 : one simply takes
: one simply takes 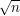 sets of aligned rectangles and makes sure that two aligned rectangles in the same set intersect, while two aligned rectangles in different sets are disjoint.
sets of aligned rectangles and makes sure that two aligned rectangles in the same set intersect, while two aligned rectangles in different sets are disjoint.
Now let us match this lower bound with an upper bound that is the same—apart from a logarithmic factor.
First, if  is an aligned rectangle, let us define
is an aligned rectangle, let us define 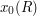 and
and 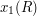 to be the minimum and maximum
to be the minimum and maximum  coordinates of points in
coordinates of points in  , respectively. Similarly, let
, respectively. Similarly, let 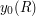 and
and 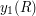 be the minimum and maximum
be the minimum and maximum 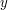 coordinates. (Thus, if
coordinates. (Thus, if  is closed, then it equals
is closed, then it equals ![[x_0(R),x_1(R)]\times[y_0(R),y_1(R)]](../images/tex/f5d0210afcaa0ad6f28c8fd9022c67b4.png) . Now, given any collection of
. Now, given any collection of  aligned rectangles, let
aligned rectangles, let  be the set of all real numbers that are equal to
be the set of all real numbers that are equal to 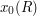 or
or 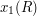 for some
for some  in the collection, and let
in the collection, and let 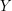 be the same thing for
be the same thing for 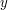 coordinates. Then the sizes of
coordinates. Then the sizes of  and
and 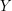 are both at most
are both at most 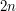 .
.
Now whether or not two rectangles  and
and 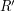 intersect depends solely on the ordering of the four numbers
intersect depends solely on the ordering of the four numbers 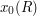 ,
, 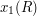 ,
, 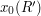 and
and 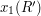 and the ordering of the four numbers
and the ordering of the four numbers 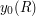 ,
, 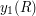 ,
, 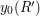 and
and 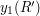 . Therefore, we can replace the sets
. Therefore, we can replace the sets  and
and 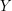 by
by 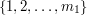 and
and 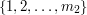 for two integers
for two integers 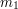 and
and 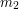 that are both at most
that are both at most 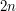 .
.
What all this amounts to is that we can assume, without loss of generality, that the coordinates of the vertices of all rectangles in the collection are integers between  and
and 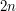 .
.
Now it turns out to be a lot easier to prove the result if all the rectangles have about the same size and shape. Here is an argument that shows that gives a lower bound of 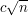 for aligned squares.◊ Let us form a graph whose vertices are the aligned squares, with an edge joining two vertices if those squares intersect. (If you are unfamiliar with graph theory terminology, then you can find it in Wikipedia's graph theory glossary.) If the maximum degree of any vertex in this graph is
for aligned squares.◊ Let us form a graph whose vertices are the aligned squares, with an edge joining two vertices if those squares intersect. (If you are unfamiliar with graph theory terminology, then you can find it in Wikipedia's graph theory glossary.) If the maximum degree of any vertex in this graph is 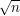 , then we can pick a sequence of vertices
, then we can pick a sequence of vertices 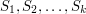 , with no vertex joined to any previous one, provided that
, with no vertex joined to any previous one, provided that 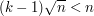 , so certainly if
, so certainly if 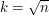 . So in this case we have a collection of
. So in this case we have a collection of 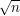 disjoint squares. But now suppose that there is a vertex of degree greater than
disjoint squares. But now suppose that there is a vertex of degree greater than 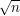 . This will be a square
. This will be a square 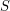 that overlaps with over
that overlaps with over 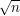 other squares. Now each of those other squares must contain a vertex of the original square (this is the step that fails when the rectangles have different shapes), so a least one vertex of
other squares. Now each of those other squares must contain a vertex of the original square (this is the step that fails when the rectangles have different shapes), so a least one vertex of 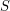 must be contained in at least
must be contained in at least 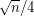 rectangles, which completes the proof.
rectangles, which completes the proof.
What can we do if we have rectangles? We can use the widely applicable trick of making everything roughly the same size. The widths of the rectangles lie between  and
and 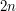 , as do their heights. Let us partition the set
, as do their heights. Let us partition the set 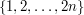 into sets of the form
into sets of the form 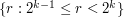 . There are at most
. There are at most 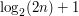 of these sets, so we can find two of them,
of these sets, so we can find two of them,  and
and  say, and a set
say, and a set 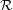 of at least
of at least 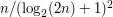 aligned rectangles taken from the original collection, such that the width of every rectangle in
aligned rectangles taken from the original collection, such that the width of every rectangle in 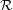 lies in
lies in  and the height lies in
and the height lies in  .
.
This implies that the ratios of the widths and heights of any two rectangles in 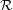 are at most 2. We now repeat the argument above for squares, except that this time when we have a rectangle
are at most 2. We now repeat the argument above for squares, except that this time when we have a rectangle  of degree at least
of degree at least 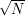 (where
(where 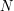 is the size of
is the size of 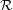 ), we cannot argue that all rectangles that intersect
), we cannot argue that all rectangles that intersect  must contain a vertex of
must contain a vertex of  . However, we can argue that any rectangle in
. However, we can argue that any rectangle in 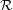 that intersects
that intersects  contains either a vertex of
contains either a vertex of  or the midpoint of an edge or the centre of
or the midpoint of an edge or the centre of  . This makes nine possibilities, so we can obtain a lower bound of
. This makes nine possibilities, so we can obtain a lower bound of 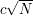 . Since
. Since 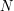 is of the form
is of the form 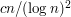 , this gives a lower bound of the form
, this gives a lower bound of the form 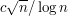 for the original problem.
for the original problem.
This demonstrates one way in which stray logarithmic factors can arise: through an application of the make-everything-roughly-the-same-size trick.
It is often possible to be more careful and remove a logarithmic factor of this kind by avoiding the use of that trick and thinking hard about how to relate objects of different sizes. However, closing the gap between the above estimates is still an open problem.
 Tricki
Tricki
Comments
Squares?
Fri, 02/03/2012 - 12:41 — lkozmaIn the example proof, instead of squares, isn't it meant to be rectangles equal to each other? If squares are allowed to have different sizes, I don't think it is true that each neighbour of a square must overlap with one of its vertices.
A question: is there some reference for this problem and proof? I realize this problem asks for bounds on m in terms of n, where n=R(m,m) for intersection graph of rectangles. Was this studied for other special graphs?
Inline comments
The following comments were made inline in the article. You can click on 'view commented text' to see precisely where they were made.
Only if squares are of the
Fri, 02/03/2012 - 12:43 — lkozmaOnly if squares are of the same size, no? It would also work for rectangles with same sizes, right?
Post new comment
(Note: commenting is not possible on this snapshot.)