 |
Rough idea of unwritten article
Often it is easier to deal with objects that are roughly the same size. If the range of sizes isn't too great, then we can achieve this by picking a large subset of the objects we have at hand, or partitioning them into not too many sets. For example, if the integers 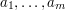 all lie between
all lie between  and
and  , we can partition them into at most
, we can partition them into at most 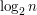 sets such that any two
sets such that any two 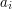 in the same cell of the partition are within a factor of 2 of each other. This very simple trick is very useful, though it often comes at the expense of extra logarithmic factors in proofs.
in the same cell of the partition are within a factor of 2 of each other. This very simple trick is very useful, though it often comes at the expense of extra logarithmic factors in proofs.
It would definitely be good if someone could write this article, and even better if they can think of a good way of classifying the article—it is not altogether obvious how to do so, as the basic idea is used in many different contexts. But how would somebody who needed it stumble on it in the Tricki?
 Tricki
Tricki
Comments
Dyadic pigeonhole principle
Thu, 16/04/2009 - 18:40 — taoI wrote something on this (the "dyadic pigeonhole principle") at
http://www.math.ucla.edu/~tao/preprints/Expository/pigeonhole.dvi
I may try to convert this to the wiki format, but probably not soon.
Post new comment
(Note: commenting is not possible on this snapshot.)