Quick description
Evaluation maps provide a tool for understanding how one representation (of a group, say, or of a ring) can appear in another. The basic idea is as follows:
suppose that  and
and  are representations of a group
are representations of a group  (over a field
(over a field  ,
say). How could we tell
if
,
say). How could we tell
if  appears as a subrepresentation of
appears as a subrepresentation of  ? Well, if it does, there will
certainly be a
? Well, if it does, there will
certainly be a  -linear
-linear  -equivariant homomorphism
-equivariant homomorphism 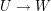 (namely, the inclusion of
(namely, the inclusion of  as a subrepresentation of
as a subrepresentation of  ). So, it makes sense to look
at the
). So, it makes sense to look
at the  -vector space
-vector space ![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) of all
of all  -linear
-linear
 -equivariant maps from
-equivariant maps from  to
to  .
Any such homomorphism may be evaluated on elements of
.
Any such homomorphism may be evaluated on elements of  to yield elements
of
to yield elements
of  , and so we get a map
, and so we get a map
![U \times \mathrm{Hom}_{k[G]}(U,W) \rightarrow W;](../images/tex/cf04b6a0aeec0412b67e129de621a4f8.png)
precisely, this map is defined by
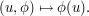 This map is evidently
This map is evidently  -bilinear, and so tautologically
gives rise to a
-bilinear, and so tautologically
gives rise to a  -linear map on the tensor product
-linear map on the tensor product
![U\otimes_k \mathrm{Hom}_{k[G]}(U,W) \rightarrow W,](../images/tex/d503320daa5ca9a4f986c2217009d550.png)
defined by 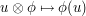 .
We call this map
the evaluation map.
.
We call this map
the evaluation map.
Note that the source and target of this map both have  -actions: on
the source, there is the action induced by the action on
-actions: on
the source, there is the action induced by the action on  , while
on the target, there is the action on
, while
on the target, there is the action on  . Furthermore, one checks
that the evaluation map is
. Furthermore, one checks
that the evaluation map is  -equivariant. Simply compute that
-equivariant. Simply compute that
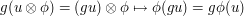 .
It provides a tautological
measurement of the relationship between the representations
.
It provides a tautological
measurement of the relationship between the representations  and
and  .
For example, it is non-zero if and only if some non-zero quotient of
.
For example, it is non-zero if and only if some non-zero quotient of  embeds
as a subrepresentation of
embeds
as a subrepresentation of  . By imposing various conditions on
. By imposing various conditions on  and
and  , one can draw various conclusions of differing degrees of strength.
, one can draw various conclusions of differing degrees of strength.
One important point is that the formation of ![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) is functorial (equivalently, natural) in
is functorial (equivalently, natural) in  and
and  , and so if
, and so if  or
or  have any extra structure, this structure is inherited by
have any extra structure, this structure is inherited by
![\mathrm{Hom}_{k[G]}(U,W).](../images/tex/3aa9e8db7ead943c1fcf6d1ba3c2aec4.png) We will see applications of this in the examples
below.
We will see applications of this in the examples
below.
Prerequisites
Basic graduate level algebra, including tensor products and representation theory.
Example 1
Before we study more general examples of evaluation maps, it will be helpful to study the structure of the source of the evaluation map.
Suppose to begin with that  is a finite-dimensional irreducible
is a finite-dimensional irreducible  -representation over an algebraically closed field
-representation over an algebraically closed field  . If
. If  is a
is a  -vector space, then the tensor product
-vector space, then the tensor product 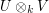 is equipped with a
is equipped with a  -action (via the
-action (via the  -action on the first factor),
and so is naturally a
-action on the first factor),
and so is naturally a  -representaiton over
-representaiton over  .
.
What does it look like?
Well, if we choose a basis 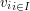 of
of  , then we obtain
an isomorphism
, then we obtain
an isomorphism 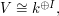 and hence an isomorphism of
and hence an isomorphism of
 -representations
-representations 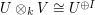 . So
. So 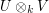 is just a direct sum of copies of
is just a direct sum of copies of  . However, the basis
. However, the basis 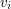 of
of 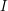 is not canonical. On the other hand, the
is not canonical. On the other hand, the  -vector space
-vector space  is canonically
determined by the representation
is canonically
determined by the representation 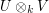 , as the following result shows.
, as the following result shows.
Proof of Theorem 1. Tensoring with  induces a canonical map
induces a canonical map
![\mathrm{Hom}_{k[G]}(U,U)\otimes_k V \rightarrow \mathrm{Hom}_{k[G]}(U, U\otimes_k V),](../images/tex/6bb8946e44f09a1861286d9506b5bf79.png)
which we claim is an isomorphism.
To check this, we can compute this map after choosing a basis
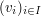 of
of  .
It then becomes identified with the natural map
.
It then becomes identified with the natural map
![\mathrm{Hom}_{k[G]}(U,U)^{\oplus I} \rightarrow \mathrm{Hom}_{k[G]}(U,U^{\oplus I}),](../images/tex/c4837cafb15f35e131b43cf2a629101d.png)
which is immediately seen to be an isomorphism.
Now since  is algebraically closed and
is algebraically closed and  if finite-dimensional,
Schur's lemma shows that
if finite-dimensional,
Schur's lemma shows that
![\mathrm{Hom}_{k[G]}(U,U) = k](../images/tex/ba6751d21a6c358dddf3f14f31edb388.png) . Since
. Since 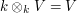 ,
we obtain the required isomorphism
,
we obtain the required isomorphism
![V \cong \mathrm{Hom}_{k[G]}(U,U\otimes_k V).](../images/tex/69d1e70dc9e885f02f31431d56a1f869.png) After identifying
After identifying  and
and ![\mathrm{Hom}_{k[G]}(U,U\otimes_k V)](../images/tex/9b6dd39706971c6cfad20548dd48eb0c.png) via this isomorphism, the evaluation map
becomes the identity map
via this isomorphism, the evaluation map
becomes the identity map 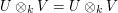 ,
and thus the evaluation map is seen to be an isomorphism, as claimed.□
,
and thus the evaluation map is seen to be an isomorphism, as claimed.□
We have seen that unlike the indexing set 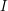 , the vector space
, the vector space  is canonically determined by
is canonically determined by 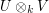 . Still, it is reasonable
to ask
what advantage comes from describing our representation in the
form
. Still, it is reasonable
to ask
what advantage comes from describing our representation in the
form 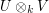 , rather than just explicitly as the direct sum
, rather than just explicitly as the direct sum
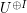 ? Well, here is one advantage:
suppose that
? Well, here is one advantage:
suppose that  is any subrepresentation
of
is any subrepresentation
of 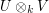 . Then one can show that
. Then one can show that  is also isomorphic
to a direct sum of copies of
is also isomorphic
to a direct sum of copies of  , say
, say  .
But the subset
.
But the subset 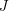 need not be in any natural way a subset of
need not be in any natural way a subset of 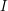 .
(Just as we may not in general be able to choose the basis of a subspace of a given vector space to
be a subset of some particular fixed basis of the entire space.)
On the other hand, we have the following result.
.
(Just as we may not in general be able to choose the basis of a subspace of a given vector space to
be a subset of some particular fixed basis of the entire space.)
On the other hand, we have the following result.
Proof of Theorem 2. Let  be a subrepresentation.
Since (as we remarked above)
be a subrepresentation.
Since (as we remarked above)  is isomorphic to a direct sum of copies of
is isomorphic to a direct sum of copies of  ,
we may write
,
we may write  for some set
for some set 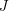 . Thus Theorem 1 shows that
the evaluation map
. Thus Theorem 1 shows that
the evaluation map ![U\otimes_k \mathrm{Hom}_{k[G]}(U,W) \rightarrow W](../images/tex/04458ad8fffb8c72bc6c23469af53bcc.png) is an isomorphism. On the other hand, since
is an isomorphism. On the other hand, since 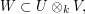 we have a corresponding inclusion
we have a corresponding inclusion
![\mathrm{Hom}_{k[G]}(U,W) \subset \mathrm{Hom}_{k[G]}(U,U\otimes_k V).](../images/tex/c06bf2c9bb0e84c2333c4e5efcbeb8dc.png) Hence, if we write
Hence, if we write ![= \mathrm{Hom}_{k[G]}(U,W),](../images/tex/f6a63f60f2474504c8b98481401113f5.png) and use
Theorem 1 to identify
and use
Theorem 1 to identify ![\mathrm{Hom}_{k[G]}(U,U\otimes_k V)](../images/tex/9b6dd39706971c6cfad20548dd48eb0c.png) ◊
with
◊
with  , we see that we may regard
, we see that we may regard 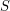 as a subspace of
as a subspace of  ,
and that the evaluation map identifies
,
and that the evaluation map identifies 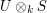 with
with  ,
as claimed.□
,
as claimed.□
Example 2
Suppose that  and
and  are representation of the group
are representation of the group  over an algebraically closed field
over an algebraically closed field  , with
, with  irreducible. Then
irreducible. Then
![\mathrm{Hom}_{k[G]}(V,W)](../images/tex/78479eac92a58bf1357766a48ab5e81c.png) is called the multiplicity space of
is called the multiplicity space of  in
in  .
It measures how many independent copies of
.
It measures how many independent copies of  appears as subrepresentations
of
appears as subrepresentations
of  . More precisely, we have the following theorem.
. More precisely, we have the following theorem.
![V \otimes_k \mathrm{Hom}_{k[G]}(V,W) \rightarrow W](../images/tex/c795dd198783d39df1dce7f0ff340550.png)
 that are isomorphic to
that are isomorphic to  , or equivalently, the maximal subrepresentation
of
, or equivalently, the maximal subrepresentation
of  that is isomorphic to a direct sum of copies of
that is isomorphic to a direct sum of copies of  .
.Proof of Theorem 3. If 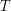 is any irreducible subrepresentation of
is any irreducible subrepresentation of  isomorphic to
isomorphic to
 , then there is an isomorphism
, then there is an isomorphism 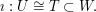 Thus the image of
Thus the image of 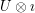 under the evaluation map
is equal to
under the evaluation map
is equal to 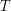 , and thus the image of the evaluation map
contains the sum of all subobjects isomorphic to a direct sum
of copies of
, and thus the image of the evaluation map
contains the sum of all subobjects isomorphic to a direct sum
of copies of  . Thus it contains their sum. Denote this
sum by
. Thus it contains their sum. Denote this
sum by  ; it is a subrepresentation of
; it is a subrepresentation of  contained in the
image of the evaluation map.
contained in the
image of the evaluation map.
On the other hand, ![U\otimes_k \mathrm{Hom}_{k[G]}(U,V)](../images/tex/cb7b7ac118fb9b7e6fb12d2a4f6aeaaf.png) is isomorphic to a direct sum of copies of
is isomorphic to a direct sum of copies of  , and so certainly its image under the evaluation
map is a sum of copies of subrepresentations isomorphic to
, and so certainly its image under the evaluation
map is a sum of copies of subrepresentations isomorphic to  . Hence its
image is contained in
. Hence its
image is contained in  . Consequently, we see that the image of the
evaluation map is precisely equal to
. Consequently, we see that the image of the
evaluation map is precisely equal to  . We also see that the inclusion
. We also see that the inclusion
![\mathrm{Hom}_{k[G]}(U,X) \subset \mathrm{Hom}_{k[G]}(U,V)](../images/tex/67758e8e255c2e1e92bb067d67269a91.png) is in fact an
equality.
Thus to complete the proof of the theorem, it suffices to show
that
is in fact an
equality.
Thus to complete the proof of the theorem, it suffices to show
that  is isomorphic to a direct sum of copies of
is isomorphic to a direct sum of copies of  , since
Theorem 1 will then imply that the
evaluation map
, since
Theorem 1 will then imply that the
evaluation map
![U\otimes_k \mathrm{Hom}_{k[G]}(U,X) \rightarrow X](../images/tex/3a4b27d65e0b5b42fbff6d3e9bfa1a6a.png)
is an isomorphism.
If we let 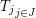 denote the collection of all subrepresentations
denote the collection of all subrepresentations
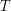 of
of  that are isomorphic to
that are isomorphic to  (thus
(thus 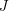 is an index set labelling all such
is an index set labelling all such 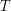 ),
then there is a canonical surjection
),
then there is a canonical surjection
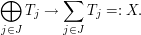
Now 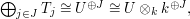 and thus Theorem 2 shows that the kernel of the above surjection
has the form
and thus Theorem 2 shows that the kernel of the above surjection
has the form 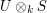 for some subspace
for some subspace 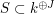 .
Thus
.
Thus  is isomorphic to
is isomorphic to
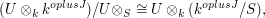
and so is indeed isomorphic to a direct sum of copies of  .
As we already remarked, this completes the proof.□
.
As we already remarked, this completes the proof.□
Example 3
Suppose that  and
and  are two groups.
are two groups.
 (respectively
(respectively
 ) is a finite-dimensional
irreducible representation of
) is a finite-dimensional
irreducible representation of  (respectively of
(respectively of  )
over an algebraically closed field
)
over an algebraically closed field  , then the tensor product
, then the tensor product
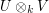 , with the natural
, with the natural 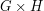 -action induced by
the
-action induced by
the  -action on
-action on  and the
and the  -action on
-action on  , is an irreducible
, is an irreducible
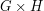 -representation.
-representation.Proof of Theorem 4. Suppose that  is a
is a 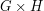 -subrepresentation of
-subrepresentation of 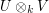 .
Thinking of
.
Thinking of  simply as a
simply as a  -subrepresentation for the moment,
Theorem 2 shows that
-subrepresentation for the moment,
Theorem 2 shows that  has the form
has the form 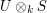 for some
for some 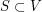 . Moreover, since
. Moreover, since  is in fact a
is in fact a
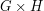 -subrepresentation of
-subrepresentation of 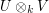 , we see that
, we see that 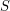 must be an
must be an  -invariant subspace of
-invariant subspace of  , i.e. an
, i.e. an  -subrepresentation
of
-subrepresentation
of  . Since
. Since  is irreducible by assumption, we see that
either
is irreducible by assumption, we see that
either 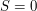 or
or 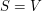 . Thus either
. Thus either 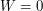 or
or 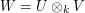 ,
and so
,
and so 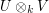 is an irreducible
is an irreducible 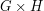 -representation,
as claimed.□
-representation,
as claimed.□
We now prove the converse of Theorem 4.
 is an irreducible finite-dimensional representation of a product of groups
is an irreducible finite-dimensional representation of a product of groups 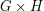 over an algebraically closed field
over an algebraically closed field  . Then
. Then  is isomorphic
to the tensor product over
is isomorphic
to the tensor product over  of
an irreducible representation of
of
an irreducible representation of  and an irreducible representation of
and an irreducible representation of  .
.Proof of Theorem 5. To begin with, think of  just as a
just as a  -representation. It may no longer
be irreducible, but we may find an irreducible
-representation. It may no longer
be irreducible, but we may find an irreducible  -subrepresentation, say
-subrepresentation, say  .
(This is where we use finite-dimensionality.) As above, we construct the
evaluation map
.
(This is where we use finite-dimensionality.) As above, we construct the
evaluation map
![U\otimes_k \mathrm{Hom}_{k[G]}(U,W)\rightarrow W.](../images/tex/2c9eee2b632209138d61af14151de55e.png)
Now since  is a
is a 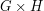 -representation, it has an action of
-representation, it has an action of  that commutes with the action of
that commutes with the action of  . (To say that
. (To say that  is endowed with
a
is endowed with
a 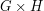 -action is just to say that it is endowed with a
-action is just to say that it is endowed with a  -action
and an
-action
and an  -action that commute with one another.) Thus this
-action that commute with one another.) Thus this  -action
on
-action
on  induces an
induces an  -action on
-action on ![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) , i.e.
, i.e.
![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) is naturally an
is naturally an  -representation.
The source of the evaluation map is then a
-representation.
The source of the evaluation map is then a 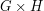 -representation
(via the
-representation
(via the  -action on the first factor and the
-action on the first factor and the  -action on the second factor).
-action on the second factor).
Since ![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) is a subspace of the space
is a subspace of the space
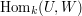 of all (not necessarily
of all (not necessarily  -equivariant)
-equivariant)  -linear
maps from
-linear
maps from  to
to  , it is finite dimensional, and so contains an irreducible
, it is finite dimensional, and so contains an irreducible
 -representation, say
-representation, say  . The tensor product
. The tensor product
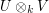 is a
is a 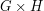 -subrepresentation of
-subrepresentation of
![U\otimes_k \mathrm{Hom}_{k[G]}(U,W),](../images/tex/5011d2e929e8bd0a502c85c24402f13b.png) and so the evaluation map restricts to give a
and so the evaluation map restricts to give a 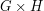 -equivariant map
-equivariant map
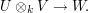
We claim that this map is non-zero: if 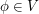 is non-zero, then it
is a non-zero map from
is non-zero, then it
is a non-zero map from  to
to  (by definition), and thus we may find
an element
(by definition), and thus we may find
an element 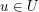 such that
such that 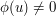 . The evaluation map
then sends
. The evaluation map
then sends 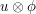 to
to 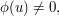 and so we see that indeed
we have a non-zero map.
and so we see that indeed
we have a non-zero map.
The preceding example shows that 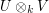 is irreducible subrepresentation
of
is irreducible subrepresentation
of 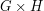 . Thus we have a non-zero map between irreducible subrepresentations of
. Thus we have a non-zero map between irreducible subrepresentations of 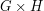 , which must thus be
an isomorphism.
Since our map is a non-zero
, which must thus be
an isomorphism.
Since our map is a non-zero 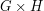 -equivariant map, its image is
a non-zero
-equivariant map, its image is
a non-zero 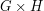 -equivariant subrepresentation of
-equivariant subrepresentation of  .
Since
.
Since  was assumed to be irreducible over
was assumed to be irreducible over 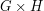 , it has no non-zero
, it has no non-zero
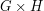 -subrepresentations other than itself, and so our map must in
fact be surjective. Since it is non-zero, its kernel is a proper
-subrepresentations other than itself, and so our map must in
fact be surjective. Since it is non-zero, its kernel is a proper 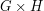 -submodule
of
-submodule
of 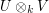 . As this is again an irreducible
. As this is again an irreducible 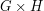 -representation,
the only proper subrepresentation that it contains is the zero representation.
Thus our map has vanishing kernel, and so is also injective.
This completes the proof.□
-representation,
the only proper subrepresentation that it contains is the zero representation.
Thus our map has vanishing kernel, and so is also injective.
This completes the proof.□
Remark
The proof of Theorem 5 brings out an important point,
namely that
if  is a representation of
is a representation of 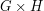 , and
, and  is a
is a
 -representation, then the space
-representation, then the space ![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) is naturally an
is naturally an  -representation. This construction is frequently
used (by making a careful choice of
-representation. This construction is frequently
used (by making a careful choice of  ) to create interesting correspondences between representations of a group
) to create interesting correspondences between representations of a group
 and of a group
and of a group  .
.
We illustrate this remark further with some more examples.
Example 4
 |
Let 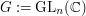 , the matrix group of invertible
, the matrix group of invertible 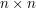 -matrices
over
-matrices
over 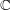 , and
, and  to be the symmetric group
to be the symmetric group 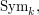 for some
for some
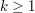 . The group
. The group  has a natural representation on
has a natural representation on 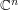 , namely the usual action
of
, namely the usual action
of 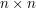 -matrices on length
-matrices on length  column vectors. If we take
column vectors. If we take
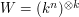 , then permuting the factors
in the tensor product gives a representation of
, then permuting the factors
in the tensor product gives a representation of
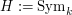 on
on  , commuting with the
, commuting with the  -action.
Thus
-action.
Thus  is a
is a 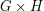 -representation, and the map
-representation, and the map
![U \mapsto \mathrm{Hom}_{\C[G]}(U,W)](../images/tex/584dd7731dd944651567808141c01ff3.png) gives a map from (isomorphism classes of)
irreducible
gives a map from (isomorphism classes of)
irreducible  -representations to (isomorphism classes of)
-representations to (isomorphism classes of)  -representations.
It turns out that the multiplicity space
-representations.
It turns out that the multiplicity space ![\mathrm{Hom}_{\C[G]}(U,W)](../images/tex/7af7c1521c127838d38ad877a3a4c73a.png) is irreducible
as an
is irreducible
as an  -representation (if it is non-zero), and this construction gives
a bijection bewteen those irreducible representations of
-representation (if it is non-zero), and this construction gives
a bijection bewteen those irreducible representations of  which embed
into
which embed
into  , and certain irreducible representations of
, and certain irreducible representations of  . (If
. (If 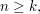 then in fact every irreducible representation of
then in fact every irreducible representation of  arises in this way.)
This is known as Schur-Weyl duality.
arises in this way.)
This is known as Schur-Weyl duality.
Example 5
Here are two more very briefly sketched examples, both at a much more advanced level than the rest of this article:
In the context of the Langlands program,
one can take  to be the finite adélic points
of some reductive linear algebraic group over
to be the finite adélic points
of some reductive linear algebraic group over 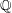 ,
,  to be an appropriately
chosen Galois
group, and
to be an appropriately
chosen Galois
group, and  to be a representation of
to be a representation of 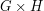 constructed out
of the cohomology of a Shimura variety attached to
constructed out
of the cohomology of a Shimura variety attached to  .
One will take
.
One will take  to be (the finite part of) an irreducible automorphic
representation of the group
to be (the finite part of) an irreducible automorphic
representation of the group  . The passage from
. The passage from  to
to
![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) will then give a construction of Galois representations
associated to automorphic representations.
will then give a construction of Galois representations
associated to automorphic representations.
In the general theory of theta functions, one takes
 and
and  to be the members of
a dual reductive pair
of groups, and
to be the members of
a dual reductive pair
of groups, and  is a certain Weil representation.
The resulting passage from
is a certain Weil representation.
The resulting passage from  -representations to
-representations to  -representations
is then referred to as the theta correspondence.
-representations
is then referred to as the theta correspondence.
 Tricki
Tricki![V \cong \mathrm{Hom}_{k[G]}(U,U\otimes_k V),](../images/tex/20d3c166aee0ea9536688c09b1c9ad1a.png)
![U\otimes_k \mathrm{Hom}_{k[G]}(U,U\otimes_k V) \rightarrow U\otimes_k V](../images/tex/eecc75325efc00ac5de48c5cf33d4076.png)
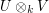
Comments
"The proof of Theorem 5
Sun, 26/04/2009 - 13:58 — Anonymous (not verified)"The proof of Theorem 5 brings out an important point, namely that if W is a representation of G\times H, and U is an irreducible G-representation, then"
You are correct, but then one
Mon, 27/04/2009 - 02:26 — emertonYou are correct, but then one probably shouldn't use the term "multiplicity space" to describe![\mathrm{Hom}_{k[G]}(U,W)](../images/tex/5b2f77f5cf594bee746a93051d45023a.png) . I will make an edit that reflects your comment.
. I will make an edit that reflects your comment.
Does Theorem 1 require that U
Tue, 26/05/2009 - 13:57 — Anonymous (not verified)Does Theorem 1 require that U is simple? The proof (use of Schur's lemma) seems to assume this.
Yes. The preamble to the
Mon, 01/06/2009 - 03:18 — emertonYes. The preamble to the theorem states that is finite dimensional and irreducible. If you want to makes these conditions explicit in the statement of the theorem, feel free to add them.
is finite dimensional and irreducible. If you want to makes these conditions explicit in the statement of the theorem, feel free to add them.
Inline comments
The following comments were made inline in the article. You can click on 'view commented text' to see precisely where they were made.
2 typos in Proof of Theorem 2
Wed, 09/09/2009 - 18:44 — maexe (not verified)In Proof of Theorem 2:
... use Theorem 1 to identify \mathrm{Hom}_{k(G)}(U,U \otimes_k V) with V (not U),
we see that we may regard S as a subspace of V (not U).
Beyond this, a very nice article.
Post new comment
(Note: commenting is not possible on this snapshot.)