Quick description
The tensor product is a way to encapsulate the notion of bilinearity, and can be thought of as a multiplication of two vector spaces.
Prerequisites
Linear algebra.
See also
 |
General discussion
The dimension of a tensor product of two vector spaces is precisely the product of their dimensions, so when one wishes to show that a certain vector space is finite dimensional, one can try to show that it is a subspace of a tensor product (or an image of a tensor product) of two finite dimensional vector spaces.
Example 1
Fix a field 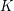 . Some notation:
. Some notation: ![K[x]](../images/tex/a77a9131b3530308247cff0e3c92321a.png) is the polynomial ring in one variable,
is the polynomial ring in one variable, 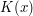 is the field of rational functions,
is the field of rational functions, ![K[ [ x ] ]](../images/tex/20b2caed4698f6de0d2e6332f6164f49.png) is the ring of formal power series, and
is the ring of formal power series, and 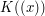 is the field of formal Laurent series.
is the field of formal Laurent series.
A power series ![u \in K[ [ x ] ]](../images/tex/c1a563eca11c7543784ee7bdd0f96248.png) is said to be D-finite if it satisfies a linear differential equation
is said to be D-finite if it satisfies a linear differential equation 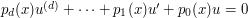 for some polynomials
for some polynomials ![p_i(x) \in K[x]](../images/tex/1eae70ba73a9cd891ab52ff79926f05d.png) with
with 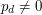 , and
, and 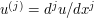 . Let
. Let 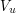 denote the
denote the 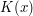 -subspace of
-subspace of 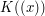 spanned by the derivatives of
spanned by the derivatives of  . Then the property of being D-finite can be seen to be equivalent to requiring that the subspace
. Then the property of being D-finite can be seen to be equivalent to requiring that the subspace 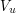 is finite dimensional over
is finite dimensional over 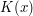 . From this, it is easy to see that the sum of two D-finite generating functions is also D-finite since
. From this, it is easy to see that the sum of two D-finite generating functions is also D-finite since 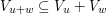 . But what about the product of two D-finite generating functions?
. But what about the product of two D-finite generating functions?
We can define a map 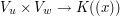 by multiplication: the pair
by multiplication: the pair 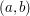 simply goes to
simply goes to 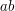 . The subspace spanned by the image of this will contain
. The subspace spanned by the image of this will contain 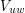 by the Leibniz rule for taking the derivative of a product. But this map is not linear, so we cannot say much about the dimension of this span. However, it is bilinear, and hence we have an associated linear map
by the Leibniz rule for taking the derivative of a product. But this map is not linear, so we cannot say much about the dimension of this span. However, it is bilinear, and hence we have an associated linear map 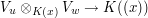 whose image is precisely the span of the image of the bilinear map, and we see then that
whose image is precisely the span of the image of the bilinear map, and we see then that 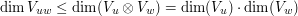 , so
, so 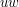 is also D-finite.
is also D-finite.
Example 2
This finite dimensionality argument is used when proving a basic result about affine algebraic groups over fields, namely that they admit a faithful linear representation (and thus are rightfully called linear algebraic groups).
An affine algebraic group 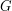 is of the form
is of the form 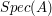 where
where 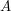 is a
is a 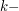 algebra of finite type endowed with a comultiplication
algebra of finite type endowed with a comultiplication 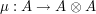 . Constructing a faithful linear representation of
. Constructing a faithful linear representation of 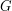 boils down to finding a surjection
boils down to finding a surjection ![k[x_{ij}]\rightarrow A](../images/tex/735ea98b4a2839e72ad8db9ffe76ad8f.png) where the polynomial ring
where the polynomial ring ![k[x_{ij}]](../images/tex/51b10835145489c8a1178eb1e93ab4e5.png) is endowed with the usual Hopf algebra structure. This is done by choosing carefully a finite set of generators of the
is endowed with the usual Hopf algebra structure. This is done by choosing carefully a finite set of generators of the 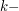 algebra
algebra 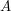 in such a way that the spanned finite dimensional
in such a way that the spanned finite dimensional 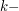 vector space
vector space 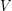 satisfies
satisfies 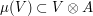 and writing down the coefficients. See e.g Borel's book Linear Algebraic Book, sections I.1.9 and I.1.10
and writing down the coefficients. See e.g Borel's book Linear Algebraic Book, sections I.1.9 and I.1.10
 Tricki
Tricki
Comments
Can the notation be
Sat, 18/04/2009 - 01:45 — anonymous (not verified)Can the notation be explained? Is![K[x]](../images/tex/a77a9131b3530308247cff0e3c92321a.png) different from
different from 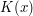 different from
different from 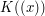 ?
?
Clarification
Tue, 21/04/2009 - 08:25 — JoseBroxAnonymous:
Usually, all those are different algebraic structures:
Post new comment
(Note: commenting is not possible on this snapshot.)