Integration by parts

This article is incomplete. The examples need to be written up.

Quick description

If $[a,b] \to \R$ are continuously differentiable functions, then

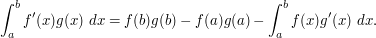
$\int_a^b f'(x) g(x)\ dx = f(b) g(b) - f(a) g(a) - \int_a^b f(x) g'(x)\ dx.$

If 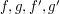$f,g,f',g'$ have sufficient decay at infinity (e.g. if they are compactly supported), then one can eliminate the boundary terms:

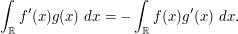
$\int_\R f'(x) g(x)\ dx = - \int_\R f(x) g'(x)\ dx.$

There are multidimensional versions, such as Stokes theorem and Greens theorem. Without boundary terms (and assuming sufficient regularity and decay), we have for instance

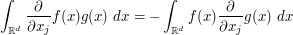
$\int_{\R^d} \frac{\partial}{\partial x_j} f(x) g(x)\ dx = - \int_{\R^d} f(x) \frac{\partial}{\partial x_j} g(x)\ dx$

for the partial derivatives 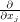$\frac{\partial}{\partial x_j}$ and scalar fields 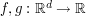$\R^d \to \R$ , as well as vector-valued variants such as

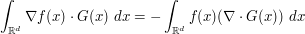
$\int_{\R^d} \nabla f(x) \cdot G(x)\ dx = - \int_{\R^d} f(x) (\nabla \cdot G(x))\ dx$

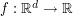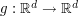for a scalar field $\R^d \to \R$ and a vector field $\R^d \to \R^d$ .

Prerequisites

Undergraduate calculus

Example 1

(Maybe integrate 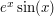$e^x \sin(x)$ by two applications of integration by parts?)

Example 2

(Use integration by parts to compute adjoints of a differential operator)

General discussion

See "use integration by parts to exploit cancellation" for one common application of integration by parts.

Integration by parts can simplify an integral by differentiating one term and integrating another. See "Which integrals are simpler to integrate" for some discussion.