Quick description
Making your method keep the symmetries of the problem means that it is immune to errors that break symmetries. This can have two important effects:
-
reducing the errors in the results, and particularly eliminating entire classes of errors that have unphysical or otherwise harmful effects,
-
and reducing the amount of computational work.
Prerequisites
Linear algebra, calculus.
Example 1
For symmetric positive definite matrices, use the Cholesky factorization rather than the LU factorization.
The LU factorization of a matrix is 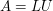 , while the Cholesky factorization is
, while the Cholesky factorization is 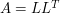 where in each case
where in each case 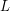 is lower triangular and
is lower triangular and 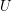 is upper triangular.
Using the Cholesky factorization (which preserves the symmetry of
is upper triangular.
Using the Cholesky factorization (which preserves the symmetry of 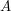 ) roughly halves the time to compute the factorization, and avoids the problems of swapping rows and/or columns of
) roughly halves the time to compute the factorization, and avoids the problems of swapping rows and/or columns of 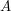 to preserve numerical stability.
to preserve numerical stability.
Example 2
Use symplectic methods to solve Hamiltonian differential equations.
A Hamiltonian differential equation has the form
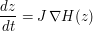
where ![J=\left[\begin{array}{cc}0&I\\ -I&0\end{array}\right]](../images/tex/78a316e3e04b42c0cf4e55b272d13c2b.png) .
Symplectic methods preserve the two-form
.
Symplectic methods preserve the two-form 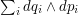 where
where ![z^T = [p^T,\, q^T]](../images/tex/89a55ab35c7de7a3c79913994bbae7d2.png) .
Such methods also nearly preserve a "numerical energy" function (which depends on the step-size), and are much better for long-time integration of mechanical systems such as arise in celestial mechanics.
.
Such methods also nearly preserve a "numerical energy" function (which depends on the step-size), and are much better for long-time integration of mechanical systems such as arise in celestial mechanics.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)