Quick description
This is a navigation page with links to articles about techniques that are useful in real analysis. See also the companion page to this one entitled I have a problem to solve in real analysis.
 |
How to use the Bolzano-Weierstrass theorem Quick description ( The Bolzano-Weierstrass theorem asserts that every bounded sequence of real numbers has a convergent subsequence. More generally, it states that if  is a closed bounded subset of
is a closed bounded subset of 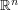 then every sequence in
then every sequence in  has a subsequence that converges to a point in
has a subsequence that converges to a point in  . This article is not so much about the statement, or its proof, but about how to use it in applications. If you come across a statement of a certain form (explained in the article), then the Bolzano-Weierstrass theorem may well be helpful. )
. This article is not so much about the statement, or its proof, but about how to use it in applications. If you come across a statement of a certain form (explained in the article), then the Bolzano-Weierstrass theorem may well be helpful. )
Constructing exotic sets and functions using limiting arguments Quick description ( If you want to construct a set or function with a strange property (for instance, you might want a function that was continuous everywhere and differentiable nowhere) then a good way of doing so is often to define your object as a limit of a sequence of objects that exhibit the behaviour you want on smaller and smaller distance scales.)
I have a problem to solve in real analysis Quick description ( This is a page that tries to understand what kind of problem you are trying to solve, so that it can take you to appropriate advice on the Tricki.)
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)