Quick description
Suppose that you have a function  that has been written as an infinite sum
that has been written as an infinite sum 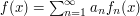 , where
, where 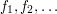 is some sequence of "nice" functions. Often it is possible to find
is some sequence of "nice" functions. Often it is possible to find  by finding a linear map
by finding a linear map  from the set
from the set 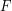 of functions you are interested in to
of functions you are interested in to 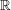 or
or 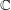 such that
such that 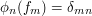 . Then
. Then 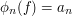 . In the language of linear algebra, it is possible in many natural problems of this kind to identify a dual basis to the basis
. In the language of linear algebra, it is possible in many natural problems of this kind to identify a dual basis to the basis 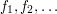 .
.
 |
Prerequisites
Basic real and complex analysis.
Example 1
Let 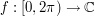 . Suppose you know that
. Suppose you know that 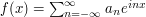 for almost every
for almost every  , with
, with 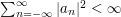 . Then
. Then
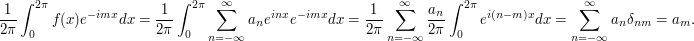
Example 2
Let  be a holomorphic function defined on some domain
be a holomorphic function defined on some domain 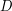 that includes the origin, and suppose that
that includes the origin, and suppose that  can be expanded in a power series
can be expanded in a power series 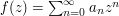 on
on 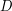 . Suppose that
. Suppose that 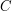 is some closed curve in
is some closed curve in 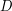 that winds once around the origin. Basic results in complex analysis (a function with an antiderivative integrates to zero round any closed curve, and the integral of
that winds once around the origin. Basic results in complex analysis (a function with an antiderivative integrates to zero round any closed curve, and the integral of 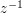 round a closed curve that winds once round the origin is
round a closed curve that winds once round the origin is 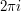 ) tell us that
) tell us that
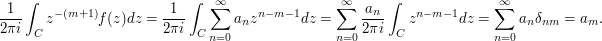
Example 3
The Lagrange interpolation formula can be derived in this way; details are at "Use basic examples to calibrate exponents".
 Tricki
Tricki
Comments
This title seems kind of
Fri, 08/05/2009 - 02:41 — Anonymous (not verified)This title seems kind of long, even for Tricki.
How about "To find the value of a coefficient, do something that kills all other terms"
I suppose I was worried that
Fri, 08/05/2009 - 08:11 — gowersI suppose I was worried that some pedant might say that making everything zero kills all other terms. But I've decided not to be worried by that after all and leave the aspect of the idea to the article itself.
aspect of the idea to the article itself.
Post new comment
(Note: commenting is not possible on this snapshot.)