Quick description
Two real numbers  and
and 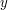 are equal if it is not the case that
are equal if it is not the case that 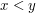 and it is not the case that
and it is not the case that 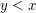 . This is often the best way to prove that
. This is often the best way to prove that 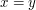 when it is not obvious.
when it is not obvious.
Example 1 (and general discussion)
This basic idea, phrased very differently, goes back at least as far as the ancient Greeks. If you want to prove that the area of a circle of radius  is
is 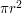 , then one way to do it is to inscribe a regular
, then one way to do it is to inscribe a regular 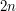 -gon. One then cuts the
-gon. One then cuts the 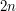 -gon into ``slices'' by joining its centre to the
-gon into ``slices'' by joining its centre to the 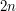 vertices, and then rearranges the slices into a parallelogram by alternating upwards-pointing slices and downwards-pointing slices. Each slice is an isosceles triangle, and the parallelogram has height the altitude of these isosceles triangles and base half the perimeter of the
vertices, and then rearranges the slices into a parallelogram by alternating upwards-pointing slices and downwards-pointing slices. Each slice is an isosceles triangle, and the parallelogram has height the altitude of these isosceles triangles and base half the perimeter of the 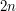 -gon.
Now let
-gon.
Now let 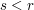 . Then if
. Then if  is large enough, the altitude of each slice will be greater than
is large enough, the altitude of each slice will be greater than  and the perimeter of the
and the perimeter of the 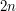 -gon will be greater than
-gon will be greater than 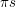 . These assertions are not trivial but are not too hard to prove geometrically. It follows that for every
. These assertions are not trivial but are not too hard to prove geometrically. It follows that for every  you can find inside the circle a polygon of area greater than
you can find inside the circle a polygon of area greater than 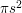 . Therefore, the area of the circle cannot be less than
. Therefore, the area of the circle cannot be less than 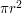 . A similar argument shows that it cannot be greater than
. A similar argument shows that it cannot be greater than 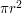 , and therefore it is equal to
, and therefore it is equal to 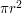 .
.
The point here is that we did not do some calculation that ended up with 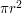 . Rather, we proved that the area could not be greater than this and could not be less than this.
. Rather, we proved that the area could not be greater than this and could not be less than this.
A similar idea is often used to prove that a non-negative number is zero: if 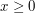 and
and 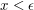 for every positive
for every positive  then
then 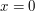 . With the help of the Archimedean principle we can also state a useful variant of this: if
. With the help of the Archimedean principle we can also state a useful variant of this: if 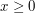 and
and 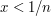 for every positive integer
for every positive integer  , then
, then 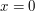 .
.
Example 2
A nice example of this is the standard proof of Liouville's theorem in complex analysis, which states that a bounded analytic function on the whole complex plane is constant. To prove this, one uses Cauchy's integral formula, which states that if  is a complex number and
is a complex number and 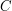 is a simple closed contour that contains
is a simple closed contour that contains  in its interior, then
in its interior, then 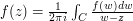 .
.
Now let  and
and 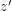 be two points and let
be two points and let 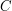 be a simple closed contour that contains both
be a simple closed contour that contains both  and
and 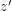 in its interior. If we now calculate
in its interior. If we now calculate 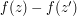 using Cauchy's integral formula, we obtain
using Cauchy's integral formula, we obtain 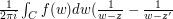 , which equals
, which equals 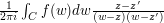 . If
. If  is bounded above in modulus by
is bounded above in modulus by 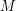 , and
, and 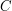 is a circle of radius
is a circle of radius  with
with  at least twice the maximum of
at least twice the maximum of 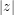 and
and 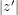 , then this comes out to be at most
, then this comes out to be at most 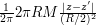 , which tends to 0 as
, which tends to 0 as  tends to infinity. Therefore,
tends to infinity. Therefore, 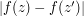 is less than any positive real number, which forces it to be zero.
is less than any positive real number, which forces it to be zero.
Example 3
One of the standard proofs of the intermediate value theorem uses the law of trichotomy in a fairly explicit way. Suppose that  is a continuous function, that
is a continuous function, that 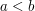 , and that
, and that 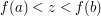 . To prove that there exists
. To prove that there exists  between
between  and
and 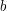 such that
such that 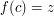 , one defines
, one defines  to be the supremum of the set
to be the supremum of the set 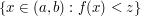 . Then instead of proving directly that
. Then instead of proving directly that 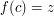 , one obtains a contradiction from the assumption that
, one obtains a contradiction from the assumption that 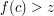 and another contradiction from the assumption that
and another contradiction from the assumption that 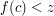 .
.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)