 |
Quick description
The Fourier transform is a powerful tool that allows one to express very general types of functions on a symmetric domain (e.g. a locally compact abelian group) in terms of special functions, such as characters. Sometimes, when studying an expression involving some function 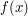 , it is often useful to expand
, it is often useful to expand  into Fourier coefficients (e.g. as Fourier series
into Fourier coefficients (e.g. as Fourier series 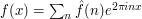 if the domain is the unit circle
if the domain is the unit circle 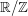 , or as Fourier integrals
, or as Fourier integrals 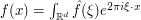 if the domain is a Euclidean space
if the domain is a Euclidean space 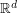 ).
).
Generally speaking, Fourier decomposition is advantageous under one of the following conditions:
-
Fourier phases already appear in the expression. If the expression already contains terms such as
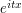 , then it is natural to try to manipulate it using, say, the Fourier inversion formula.
, then it is natural to try to manipulate it using, say, the Fourier inversion formula. -
The expression one is studying would be easier to manipulate if
 was a character. For instance, suppose one was trying to understand an expectation
was a character. For instance, suppose one was trying to understand an expectation 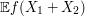 , where
, where 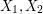 were two random variables. For arbitrary
were two random variables. For arbitrary  , there is not much one can obviously do, but if
, there is not much one can obviously do, but if  were an exponential function such as
were an exponential function such as 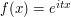 , then it looks like there is a way to separate
, then it looks like there is a way to separate 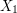 and
and 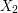 from each other. So Fourier analysis could be a useful tool here.
from each other. So Fourier analysis could be a useful tool here. -
The expression one is studying enjoys some sort of translation invariance. For instance, expressions involving convolution, constant-coefficient differential operators, addition of random variables, addition of sets in a group, or finding patterns such as arithmetic progressions, would fall into this category. Fourier analysis can be interpreted as the representation theory of the translation action, so it is reasonable to suspect that it will be a useful tool in translation-invariant settings.
-
The function
 has a particularly simple, or well understood Fourier transform. For instance, if
has a particularly simple, or well understood Fourier transform. For instance, if  lies in a Sobolev space
lies in a Sobolev space 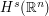 , then its Fourier transform lies in a weighted
, then its Fourier transform lies in a weighted 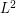 space, which is a more elementary object than
space, which is a more elementary object than 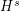 , so it can be profitable to work in the Fourier domain as much as possible when dealing with problems involving
, so it can be profitable to work in the Fourier domain as much as possible when dealing with problems involving 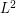 Sobolev spaces.
Sobolev spaces. -
One expects the "worst case" to be when
 behaves like a character. In such cases, taking a Fourier-analytic perspective is likely to isolate the dominant features of
behaves like a character. In such cases, taking a Fourier-analytic perspective is likely to isolate the dominant features of  , while making it easier to control all the other features.
, while making it easier to control all the other features.
Prerequisites
Fourier analysis
Example 1
(Counting additive quadruples 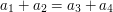 in a set)
in a set)
Example 2
(Bilinear Hilbert transform)
Example 3
(Kato local smoothing estimate for the Schrodinger equation)
Example 4
(Central limit theorem)
Example 5
(Product estimates for 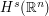 - the point is that it converts an oscillatory problem into a non-oscillatory one)
- the point is that it converts an oscillatory problem into a non-oscillatory one)
General discussion
See also "If your problem can be expressed in terms of convolutions and inner products then take the Fourier transform".
Not every translation-invariant expression is simplified by the Fourier transform. There are some expressions of "quadratic" expressions and higher which seem to require some sort of "higher-order" Fourier analysis (e.g. quadratic Fourier analysis) to control properly. The theory of higher-order Fourier analysis is not nearly as well developed as linear Fourier analysis, but is the subject of ongoing research.
 Tricki
Tricki
Comments
How would you feel about
Wed, 22/04/2009 - 09:12 — gowersHow would you feel about changing the title of this to "How to use the Fourier transform" (a title that I had put on the how-to-use wishlist)? Or is this article meant to be more specific, and just concentrating on things where applying a Fourier identity immediately simplifies your problem? In that case, "How to use the Fourier transform" could become a navigation page.
Actually, as I write this I am starting to think that the second idea is obviously better: there are so many uses of the Fourier transform, and so many perspectives on it, that it seems better to have a whole hierarchy of pages about it. Also, the top of this hierarchy might more appropriately be called "Fourier transforms front page". So what I'll do for now is create a Fourier transforms front page, which will be the page you get to when you click on "How to use the Fourier transform". And I'll make that a second parent of this article. If people don't like these decisions, they aren't set in stone.
Latest thoughts
Wed, 22/04/2009 - 15:07 — gowersI've now started an article I had planned called If your problem can be expressed in terms of convolutions and inner products then take the Fourier transform. There might be some sense in putting the additive quadruples example there, as it makes a natural first example. Or it could be both there and here. The justification for having both that article and this one (possibly overlapping) is that that one naturally links from the additive combinatorics front page and this one naturally links from estimating integrals.
Sounds good to me
Wed, 22/04/2009 - 17:53 — taoIt would be good to have different perspectives on this.
Post new comment
(Note: commenting is not possible on this snapshot.)