Quick description
In dealing with sums or integrals involving several parameters linked with constraints of the type 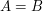 , it is often useful to rephrase these by inserting an extra sum or integral which is zero whenever the constraint is not satisfied. In particular, this may help to prove existence of solutions to certain equations by replacing the number of solutions of these equations with an analytic expression which may be successfully manipulated further.
, it is often useful to rephrase these by inserting an extra sum or integral which is zero whenever the constraint is not satisfied. In particular, this may help to prove existence of solutions to certain equations by replacing the number of solutions of these equations with an analytic expression which may be successfully manipulated further.
 |
Prerequisites
Real analysis and integration theory, complex analysis for some applications. Elementary harmonic analysis (such as Fourier transforms, or Mellin transforms, depending on the type of applications). Some knowledge of the basic properties of elementary arithmetic functions, including Möbius inversion.
General discussion
The idea of the trick is to replace expressions like
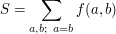
with
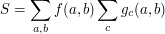
where the inner sum has the property that it represents analytically the "Kronecker delta symbol" 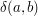 . Recall that
. Recall that 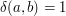 if
if 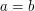 , while
, while 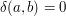 if
if 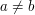 .
.
The sum over  is often interpreted in terms of harmonic analysis as a sum over suitable harmonics. Different choices might be available, and a crucial part of the argument might be to select the "right" harmonics for the situation at hand. In that case, the relations (Delta symbol) are frequently examples of orthogonality relations.
is often interpreted in terms of harmonic analysis as a sum over suitable harmonics. Different choices might be available, and a crucial part of the argument might be to select the "right" harmonics for the situation at hand. In that case, the relations (Delta symbol) are frequently examples of orthogonality relations.
To go further, one typically will interchange the sums, getting
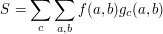
and then one has to be able to say something about the inner sums. Often, the issue of uniformity with respect to the "harmonic"  will be crucial. Also, it often turns out that there is a "special" harmonic
will be crucial. Also, it often turns out that there is a "special" harmonic 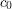 for which the sum
for which the sum
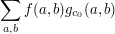
is particularly easy to work with, and may represent a "main term" for counting the solution to some equation. Then the main work is to establish that the other sums
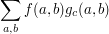
are of smaller order of magnitude for 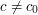 .
.
It is not necessarily the case that two variables (or more) are involved; similar tricks can be useful to express analytically a single condition (see for instance Example 2).
Example 1: Detecting coprimality conditions
Very often in analytic number theory, one has to deal with (positive) integer variables related by a condition that they be coprime. The Möbius identity below gives a way of treating such conditions.
As an example, a classical question is: "What is the probability that two positive integers be coprime?" Although it is not a probability in the modern sense (and "density" might be a better word), is it somewhat natural to identify this with the limit, as 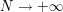 , if it exists, of
, if it exists, of
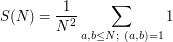
where 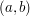 denotes the gcd of the positive integers
denotes the gcd of the positive integers  and
and 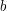 .
.
The conditions 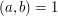 can be detected by the Möbius function
can be detected by the Möbius function 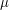 which is defined by
which is defined by 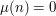 if
if  is divisible by the square of a prime, and otherwise
is divisible by the square of a prime, and otherwise 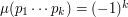 for distinct primes
for distinct primes 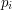 , and
, and 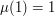 , through the formula
, through the formula
where 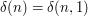 tells whether a positive integer is equal to
tells whether a positive integer is equal to  or not. (This formula is a special case of the Möbius inversion formula).
or not. (This formula is a special case of the Möbius inversion formula).
Inserting this with 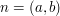 in the sum
in the sum 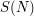 and continuing by interchanging the sum, we obtain
and continuing by interchanging the sum, we obtain
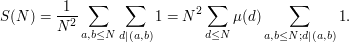
For a fixed 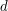 , the inner sum counts pairs of integers up to
, the inner sum counts pairs of integers up to 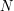 which are both divisible by
which are both divisible by 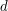 , so it is equal to
, so it is equal to 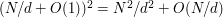 , uniformly for all
, uniformly for all 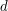 , and this gives
, and this gives
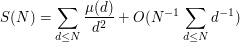
Since it is well known that
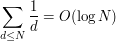
and that
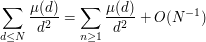
we see that
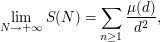
and this is therefore the intuitive probability that two positive integers be coprime. (It is also well-known that
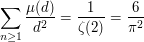
but this is not needed to prove the existence of the limit).
Note. The equation (Möbius identity) is the most common way to treat sums involving coprimality conditions of the variables in analytic number theory. It should be the first thing to try whenever such a condition arises.
Example 2: Detecting squarefreeness
This example is quite similar to the previous one. We now wish to incorporate the constraint that a positive integer  be squarefreewhich means that it is not divisible by
be squarefreewhich means that it is not divisible by 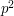 for any prime number
for any prime number  and for this we use the Möbius function again by writing
and for this we use the Möbius function again by writing
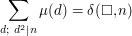
which is  if
if  is the square of an integer, and
is the square of an integer, and 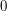 otherwise. For instance, for
otherwise. For instance, for 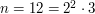 , the sum is
, the sum is 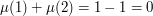 , and for
, and for 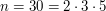 , it is
, it is 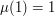 .
.
As an example, consider the probability that 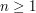 be squarefree, interpreted as the limit of
be squarefree, interpreted as the limit of
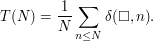
Introducing the expression above, and exchanging the sum, we obtain
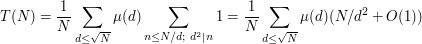
and therefore
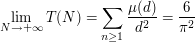
(again!)
Example 3: Detecting congruence conditions
To compute a sum
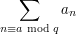
restricted by a congruence condition, one may use the orthogonality relations
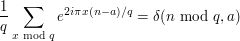
for "additive" characters.
If, in addition, the sequence 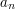 is supported on integers coprime with
is supported on integers coprime with 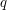 , one may instead use "multiplicative" characters: those are the group homomorphisms
, one may instead use "multiplicative" characters: those are the group homomorphisms
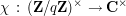
from the finite group of integers coprime with 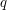 to the multiplicative group of non-zero complex numbers. There are
to the multiplicative group of non-zero complex numbers. There are 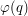 distinct such homomorphisms, where
distinct such homomorphisms, where 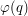 is the Euler function (the cardinality of
is the Euler function (the cardinality of 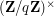 ), and the corresponding orthogonality relation is
), and the corresponding orthogonality relation is
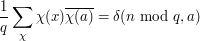
for  coprime with
coprime with 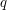 .
.
This relation is used for instance in proofs of Dirichlet's Theorem that there are infinitely many primes 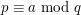 if
if 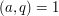 : one starts by writing that
: one starts by writing that
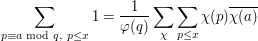
and then the inner sums are studied (for instance using Dirichlet generating series).
Example 4: Orthogonality relations
The previous example involves a special case, corresponding to finite cyclic groups, of using the orthogonality relations of characters of a finite group  to expand the delta function at the identity of
to expand the delta function at the identity of  in terms of irreducible characters.
in terms of irreducible characters.
For a finite group  , an irreducible linear representation of
, an irreducible linear representation of  is a group homomorphism
is a group homomorphism
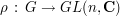
for some  , or equivalently an action of
, or equivalently an action of  on
on 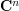 by linear automorphisms, such that there is no subspace
by linear automorphisms, such that there is no subspace 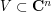 , except
, except 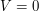 and
and 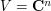 , which is invariant under all operators
, which is invariant under all operators 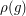 ,
, 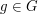 .
.
Two such representations 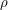 and
and  are said to be equivalent if there exists map
are said to be equivalent if there exists map 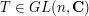 such that
such that
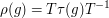
for all 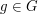 . It is known that, up to equivalence, there are only finitely many irreducible linear representations of
. It is known that, up to equivalence, there are only finitely many irreducible linear representations of  , in fact exactly as many as there are conjugacy classes in
, in fact exactly as many as there are conjugacy classes in  . They are in fact characterized by their characters, which are the functions
. They are in fact characterized by their characters, which are the functions
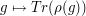
(clearly, those functions are the same for equivalent representations). Those characters provide a decomposition of the Dirac delta at the identify  of the group
of the group
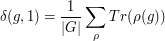
for all 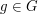 , where the sum runs over all irreducible linear representations of
, where the sum runs over all irreducible linear representations of  up to conjugacy.
up to conjugacy.
This type of decomposition is very useful, for instance, in applications of the Chebotarev Density Theorem.
Example 5: The Circle Method
The circle method is based on the use of the orthogonality relations on the circle (or equivalently, for  -periodic functions) to detect equalities: for an integer
-periodic functions) to detect equalities: for an integer 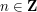 , we have
, we have
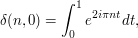
and therefore, for arbitrary integer-valued functions  and
and 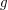 , the number
, the number 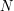 of solutions of the equation
of solutions of the equation
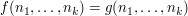
with, for instance, 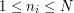 , is given by
, is given by
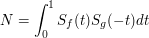
where
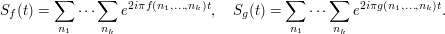
Since the set of harmonics (the whole circle 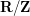 , identified with the interval
, identified with the interval 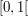 ) is not discrete, one can not isolate a single specific point to give a main term. However, the basic idea of the Circle Method, as developed by Hardy and Ramanujan to estimate the partition function, and by Hardy and Littlewood to solve the Waring Problem (i.e., solving the equation
) is not discrete, one can not isolate a single specific point to give a main term. However, the basic idea of the Circle Method, as developed by Hardy and Ramanujan to estimate the partition function, and by Hardy and Littlewood to solve the Waring Problem (i.e., solving the equation
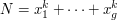
for 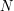 large enough,
large enough,  fixed, and
fixed, and 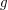 as small as possible), is that the main contributions to the integral should arise from suitable neighborhoods of rational points
as small as possible), is that the main contributions to the integral should arise from suitable neighborhoods of rational points 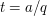 with
with 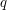 small in some sense. The quantification of this involves issues related to Dirichlet's Theorem on Diophantine approximation. There are further refinements due to Kloosterman in particular which handle the decomposition of the interval
small in some sense. The quantification of this involves issues related to Dirichlet's Theorem on Diophantine approximation. There are further refinements due to Kloosterman in particular which handle the decomposition of the interval 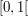 in subtler ways.
in subtler ways.
The Circle Method has also been successful, through the work of Vinogradov in particular, to solve the ternary Goldbach problem: every odd integer large enough is the sum of three primes.
For the representation theory of finite groups, the first chapters of Serre's book are the best introduction. For the Circle Method, Vaughan's tract is the best known source, and the book of Davenport (edited by T. Browning) is also highly readable. For the basic theory of arithmetic functions and the type of manipulations involving the Möbius function, Tenenbaum's book or the book of Hardy and Wright are excellent references.
 Tricki
Tricki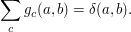
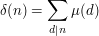
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)