Tricki
a repository of mathematical know-how

Estimating sums

Quick description

Many problems in mathematics require one to estimate a sum when it is not feasible to evaluate the sum exactly. This article contains links to articles that discuss techniques relevant to this general task.

The articles

As a first approximation, neglect lower order terms

Getting rid of nasty cutoffs

Smoothing sums

Use analytic expressions of constraints in sums or integrals

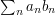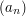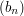Partial summation When is this useful? ( If you have a sum of the form \sum_n a_nb_n, partial summation allows you to replace the sequences (a_n) and (b_n) by the difference sequence 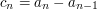c_n=a_n-a_{n-1} and the partial-sums sequence 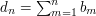d_n=\sum_{m=1}^nb_m. Partial summation is useful if the sum 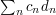\sum_nc_nd_n is easier to handle than the sum 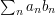\sum_na_nb_n. (It is the discrete analogue of integration by parts.))

Bounding the sum by an integral

Note iconContributions wanted This article could use additional contributions. Many more articles wanted here, starting with very basic ones on topics that would appear in a first course on analysis.

Comments

Post new comment

(Note: commenting is not possible on this snapshot.)

Before posting from this form, please consider whether it would be more appropriate to make an inline comment using the Turn commenting on link near the bottom of the window. (Simply click the link, move the cursor over the article, and click on the piece of text on which you want to comment.)

snapshot
Notifications