Quick description
Suppose you have a function 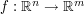 and you would like to see that
and you would like to see that  is
is 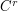 . One way to show this is to find a
. One way to show this is to find a 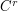 function
function 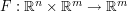 such that
such that 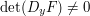 and
and
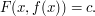
The implicit function theorem will imply that  is
is 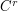 .
.
 |
Prerequisites
Calculus
Example 1
Deterministic and Stochastic Optimal Control, Wendell H. Fleming, Raymond W. Rishel, page 8. Take a 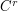 cost function
cost function 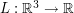 and consider the calculus of variation problem of minimizing
and consider the calculus of variation problem of minimizing
over piecewise
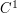 functions
functions  with the given fixed end points
with the given fixed end points 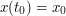 and
and
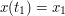 . A piecewise
. A piecewise 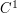 function
function  is called an extremal of (1) if it satisfies
is called an extremal of (1) if it satisfies
for 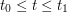 where
where  is a constant and where
is a constant and where 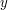 denotes the
variable of
denotes the
variable of 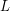 for which
for which 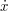 is substituted in (1) (the third variable).
is substituted in (1) (the third variable).
Now let us assume that 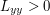 and consider an extremal
and consider an extremal  of (1) that is also
of (1) that is also 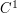 , i.e.,
, i.e., 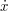 is continuous. We will show using the implicit function theorem that
is continuous. We will show using the implicit function theorem that  must be
must be 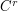 , i.e., if the extremal is
, i.e., if the extremal is 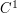 then it has to be as smooth as the cost function
then it has to be as smooth as the cost function 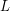 .
.
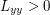 . This assumption precludes
. This assumption precludes 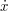 from sudden changes and forces it to be
from sudden changes and forces it to be 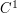 , even if this were not assumed. In order not to detract from the argument based on the implicit function theorem we assumed that
, even if this were not assumed. In order not to detract from the argument based on the implicit function theorem we assumed that  is
is 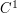 . The assumption
. The assumption 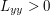 will also come into play in the invocation of the implicit function theorem.
will also come into play in the invocation of the implicit function theorem.Now let us continue with our argument that  must be as smooth as
must be as smooth as 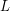 . The argument proceeds by induction. We already have the base case that
. The argument proceeds by induction. We already have the base case that  is
is 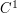 . Now let us suppose that it is
. Now let us suppose that it is 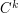 for a
for a
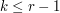 . Then
. Then
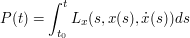
is 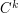 as well. By (2)
as well. By (2)
for some constant  . Define
. Define
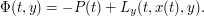
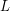 is
is 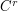 and
and 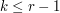 and
and  is
is 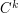 , it follows that
, it follows that
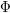 is
is 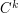 .
We can rewrite (3) as
.
We can rewrite (3) as 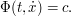
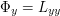 and this is strictly positive by assumption. These imply that
and this is strictly positive by assumption. These imply that
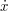 is at least as smooth as
is at least as smooth as 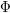 , thus
, thus 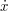 is
is 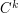 . It
follows that
. It
follows that  is
is 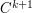 .
.
 Tricki
Tricki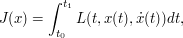
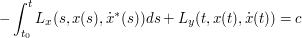
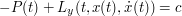
Comments
are there other examples of the argument in example one?
Sat, 25/04/2009 - 07:11 — devinThe above example has a more sophisticated method than the one I tried to describe in the quick description section. In the generalization of the method of example 1, there would be a function and the goal would be to improve our understanding of its smoothness. To that end, we use
and the goal would be to improve our understanding of its smoothness. To that end, we use  itself to define another function
itself to define another function
such that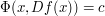 ,
, 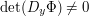 and
and 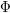 is as smooth as
is as smooth as  . Now the implicit function theorem says
. Now the implicit function theorem says 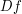 is as smooth as
is as smooth as 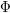 and hence
and hence  . The argument is continued as many steps as possible. Does anyone know of another application of this argument, or an argument similar to this?
. The argument is continued as many steps as possible. Does anyone know of another application of this argument, or an argument similar to this?
Notation
Thu, 07/05/2009 - 00:41 — Brendan MurphyThe notation "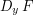 " isn't very clear. My first thought was: "partial derivative with respect to
" isn't very clear. My first thought was: "partial derivative with respect to 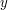 ". After this, I figured you meant the operator on
". After this, I figured you meant the operator on 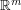 given by the decomposition of
given by the decomposition of 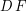 (the Jacobian of
(the Jacobian of 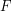 ), since this is the condition required by the theorem. Still, the notation gives rise the possibility
), since this is the condition required by the theorem. Still, the notation gives rise the possibility 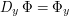 .
.
What does the notation mean in equation 2?
mean in equation 2?
Instead of using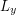 , why not use
, why not use 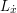 ?
?
Notation
Sat, 09/05/2009 - 15:18 — devinThanks for the comment. I like the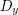 notation and frequently use it because it consisely states everything related to the operation (we are taking a derivative with respect to a variable.) The one you suggest (
notation and frequently use it because it consisely states everything related to the operation (we are taking a derivative with respect to a variable.) The one you suggest ( ) is also good I think. As for
) is also good I think. As for 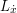 . This is common notation in many books, including Fleming and Rishel. I don't prefer it because I think it is confusing to use the same symbol to mean two entirely different things on the same page. In this case, if we use the
. This is common notation in many books, including Fleming and Rishel. I don't prefer it because I think it is confusing to use the same symbol to mean two entirely different things on the same page. In this case, if we use the 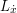 notation,
notation, 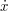 will mean the derivative of the function
will mean the derivative of the function  with respect to time and also the name of a free variable.
with respect to time and also the name of a free variable.
Post new comment
(Note: commenting is not possible on this snapshot.)