 |
Weak induction
Example 1: A simple arithmetic identity
Consider the identity Since the left-hand side of (1) is neither an arithmetic nor a geometric progression, we are unable to use the standard formulas for calculating such sums; and, indeed, it is not obvious how to transform the expression into one that can be manipulated into a formula for the sum. However, this can be proved using induction.
Example 2: The base case is important
Sometimes one can have the temptation of looking at the base case of induction as a mere formal step that is always trivially true, thinking that the "big deal" is just on the induction hypothesis. But actually it IS important: here we have an example of a general statement which induction hypothesis is true but that is always false... because we can never find a base case!
Suppose true that, for a fixed  ,
, 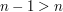 . Then,
. Then, 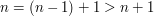 . But we obviously know that this statement is never true, so there can't be a base case.
. But we obviously know that this statement is never true, so there can't be a base case.
Strong induction
Example 3: An example of strong induction
Induction on a general ordered set
See also
Strengthen your inductive hypothesis
Transfinite induction is discussed in a separate article.
See also
Using generators and closure properties
A non-trivial circular argument can often be usefully perturbed to a non-circular one.
 Tricki
Tricki
Comments
Moved the discussion to the comments
Fri, 24/04/2009 - 20:08 — brownhWhen this article is written, it should have examples of several different styles of inductive proof: the usual kind where you deduce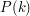 from
from 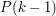 , the slightly more sophisticated kind where you deduce it from the fact that
, the slightly more sophisticated kind where you deduce it from the fact that 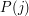 is true for every
is true for every 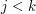 , induction over more sophisticated well-ordered sets, use of the well-ordering principle, etc.
, induction over more sophisticated well-ordered sets, use of the well-ordering principle, etc.
Induction without an indexing set
Sat, 23/05/2009 - 15:37 — Jungle"The generalized induction is harder because we don't have a nice indexing set like the natural numbers. Is there a way of doing induction without the crutch of an indexing set? Yes there is: you look for a minimal counterexample."
The above is from this article by Prof Gowers: http://www.dpmms.cam.ac.uk/~wtg10/bounded.html.
I feel that this could be put somewhere, but I am not sure where. The connection between the well-ordering principle and induction could also be mentioned (albeit briefly, since it doesn't seem like a trick).
Post new comment
(Note: commenting is not possible on this snapshot.)