 |
Quick description
Dynamic programming is a "smart exhaust," and is often used to find examples in the case where a greedy algorithm does not return an optimal result. In this article, we describe the criteria needed for a problem to posses a dynamic programming (DP) solution. We also give the general algorithm.
Prerequisites
None
Example 1
The basic example of a problem which admits a DP solution is that of finding minimal weight paths of a fixed length between vertices of a weighted, undirected graph 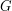 on vertices
on vertices 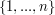 . If we write the weight between vertex
. If we write the weight between vertex 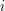 and
and 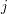 as
as 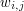 , we can collect the weights into a matrix
, we can collect the weights into a matrix 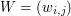 . Let
. Let 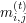 denote the minimal weight path of length
denote the minimal weight path of length 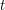 starting at vertex
starting at vertex 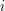 and ending at vertex
and ending at vertex 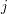 . Then we have the recurrence
. Then we have the recurrence
Here we have written path weight additively. This suggests an algorithm to determine the minimal weight paths between any two vertices:
-
Initialize
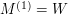
-
for
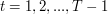 do
do-
Determine
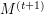 by (1).
by (1).
-
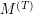 contains the weights of the minimal weight paths of length
contains the weights of the minimal weight paths of length 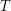 between any pair of vertices. Determining the actual paths is done in a similar manner, essentially replacing
between any pair of vertices. Determining the actual paths is done in a similar manner, essentially replacing 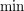 with argmin in (1). This algorithm runs in
with argmin in (1). This algorithm runs in 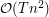 time and
time and 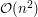 space.
space.
General discussion
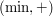 semiring (sometimes called the tropical semiring). This implies that
semiring (sometimes called the tropical semiring). This implies that 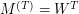 over that semiring.
over that semiring. Tricki
Tricki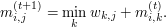
Comments
What is a "smart exhaust"?
Mon, 15/06/2009 - 23:44 — Sharon (not verified)What is a "smart exhaust"?
Post new comment
(Note: commenting is not possible on this snapshot.)