The example that sticks in my mind is proving that k-cells ![[a,b]^k](/images/tex/0ed6caf0732375180f0da789e16ef948.png) are compact. The proof is by contradiction: suppose that an open over has no finite subcover, and find a sequence of nested k-cells with no finite subcover. Eventually, one must be small enough to be covered with one neighborhood. When I first attempted the proof, I figured this much out for myself, but I didn't think to put a bound on the size of the terms and couldn't finish the proof. Now it seems like an obvious trick. (By bound, I mean set
are compact. The proof is by contradiction: suppose that an open over has no finite subcover, and find a sequence of nested k-cells with no finite subcover. Eventually, one must be small enough to be covered with one neighborhood. When I first attempted the proof, I figured this much out for myself, but I didn't think to put a bound on the size of the terms and couldn't finish the proof. Now it seems like an obvious trick. (By bound, I mean set 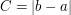 , and make the n-th interval smaller than
, and make the n-th interval smaller than 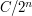 .)
.)
If this seems like a sufficiently general idea, I could write up this example. I think it needs a better title. I know I've used this trick for other problems, but I can't think of them off hand.
This proof could also be used as an example of using nested intervals (or nested compact sets), but I can think of examples where nested compact sets are used, but this bound trick isn't.
 Tricki
Tricki
Post new comment
(Note: commenting is not possible on this snapshot.)