Quick description
This method - a combination of the divide and conquer strategy and the base times height bound - is almost embarrassingly obvious: the Riemann integral 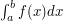 is defined to be the infimum over all sums of the form
is defined to be the infimum over all sums of the form 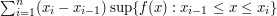 over all dissections
over all dissections 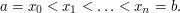 Therefore, any such sum gives us an upper bound for the integral. Often one can get useful bounds by taking very simple sums with
Therefore, any such sum gives us an upper bound for the integral. Often one can get useful bounds by taking very simple sums with  equal to 1 or 2. (When
equal to 1 or 2. (When 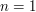 we are using the base times height technique.)
we are using the base times height technique.)
Prerequisites
First-year calculus
Example 1
The integral test for convergence is a classic example of this method: if ![[1,+\infty] \to \R^+](../images/tex/7154e82ffdbbb020fe775277e6f039d9.png) is a monotone non-increasing function, then
is a monotone non-increasing function, then 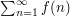 converges if and only if the integral
converges if and only if the integral 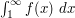 is finite. Indeed from taking upper and lower Riemann sums one obtains the bounds
is finite. Indeed from taking upper and lower Riemann sums one obtains the bounds
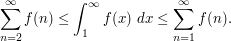
Note that this method can fail completely if  is non-monotone, and in particular if it oscillates at a wavelength significantly smaller than
is non-monotone, and in particular if it oscillates at a wavelength significantly smaller than  .
.
Example 2
Suppose you are asked to prove that the integral 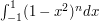 tends to
tends to 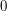 as
as  tends to infinity. One can use relatively sophisticated tools such as the monotone convergence theorem to prove this (since the pointwise limit of the functions
tends to infinity. One can use relatively sophisticated tools such as the monotone convergence theorem to prove this (since the pointwise limit of the functions 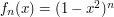 is the function that is
is the function that is 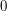 when
when ![x\in[-1,1]\setminus\{0\}](../images/tex/8e2fef83f01a18cc4aaea9860ffd5c69.png) and
and  when
when 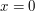 ). However, one can also prove it simply and directly as follows. We use the fact that the functions
). However, one can also prove it simply and directly as follows. We use the fact that the functions 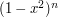 decrease as
decrease as 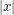 increases. Therefore, for any
increases. Therefore, for any 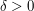 we can split the interval
we can split the interval ![[-1,1]](../images/tex/d060b17b29e0dae91a1cac23ea62281a.png) into the three parts
into the three parts ![[-1,-\delta],](../images/tex/0decdd5b7b9a8c7707330068144c4e9a.png)
![[-\delta,\delta]](../images/tex/4e568a88c79a8b3d9ab61a9f189b2fdc.png) and
and ![[\delta,1]](../images/tex/76775a33874930818683098c1badb1d2.png) and thereby obtain the upper bound
and thereby obtain the upper bound 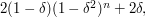 which is at most
which is at most 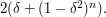 At this point, all we have to do is choose
At this point, all we have to do is choose 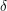 to make this quantity small. We could argue abstractly that for every
to make this quantity small. We could argue abstractly that for every 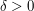 the quantity tends to
the quantity tends to 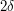 as
as 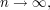 which proves the result we wanted, or we could be slightly more ambitious and try to find
which proves the result we wanted, or we could be slightly more ambitious and try to find 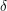 that minimizes, or at least comes close to minimizing, the expression in question.
that minimizes, or at least comes close to minimizing, the expression in question.
Let us briefly see what happens if we go for the second approach. As is often the case, if we want to have a reasonable idea of what the minimum is, we should try to choose 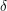 so that the two parts of the expression are equal. How do we get
so that the two parts of the expression are equal. How do we get 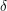 to equal
to equal 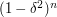 ? If
? If 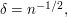 then
then 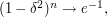 so we need to take a larger
so we need to take a larger 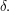 Bearing in mind that
Bearing in mind that 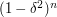 is close to
is close to 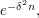 a pretty good choice is
a pretty good choice is 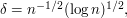 in which case
in which case 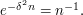 With a little bit of work, one can prove that this choice of
With a little bit of work, one can prove that this choice of 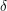 leads to an upper bound for the integral of at most
leads to an upper bound for the integral of at most 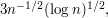 which tends to
which tends to 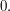
Example 3
Suppose one wants to show that the contour integral 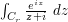 goes to zero in magnitude as
goes to zero in magnitude as 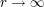 , where
, where 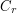 is the semicircular contour
is the semicircular contour 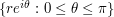 . (This is a special case of Jordan's lemma, but pretend for now that one is not aware of this lemma.) A direct application of the base times height bound, using the fact that
. (This is a special case of Jordan's lemma, but pretend for now that one is not aware of this lemma.) A direct application of the base times height bound, using the fact that 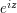 is bounded in magnitude by
is bounded in magnitude by  , gives an upper bound of the base
, gives an upper bound of the base 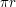 times the height
times the height 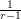 (for
(for 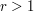 ); but unfortunately
); but unfortunately 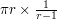 does not go to zero as
does not go to zero as 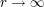 .
.
But one can do better by noting that the bound 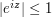 is usually quite inefficient. Indeed, if
is usually quite inefficient. Indeed, if 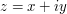 , then
, then 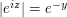 . Thus as soon as
. Thus as soon as 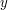 is even moderately large, e.g.
is even moderately large, e.g. 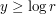 , then
, then 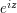 is actually quite small, e.g.
is actually quite small, e.g. 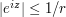 .
.
This suggests performing the following Riemann sum: in the region 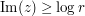 (say), use the upper bound
(say), use the upper bound 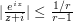 ; in the remaining region
; in the remaining region 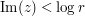 , use the cruder bound
, use the cruder bound 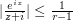 . The length of the curve in the first region can be bounded crudely by the length
. The length of the curve in the first region can be bounded crudely by the length 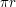 of the whole curve; meanwhile, the length of the curve in the second region can be bounded by
of the whole curve; meanwhile, the length of the curve in the second region can be bounded by 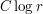 for some absolute constant
for some absolute constant 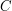 . This leads to a net upper bound of
. This leads to a net upper bound of
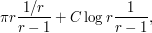
which now does successfully go to zero as 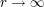 .
.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)