Quick description
This article is about a principle that often helps in proofs that functions are Riemann integrable. The idea is that if the difficulties can somehow be contained in a union of intervals of small total length, then you are OK.
Prerequisites
Basic undergraduate real analysis.
Example 1
Let ![[0,1]\rightarrow\R](../images/tex/887cfc538c4cb6e6370a98c65bf01d15.png) be defined by setting
be defined by setting 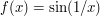 if
if 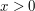 and
and 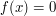 if
if 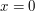 . Then
. Then  is Riemann integrable.
is Riemann integrable.
To prove this we use Riemann's criterion:  is integrable if for every
is integrable if for every 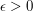 we can find a dissection
we can find a dissection  such that the upper sum
such that the upper sum 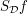 and the lower sum
and the lower sum 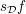 differ by at most
differ by at most  . We also use the fact that every continuous function on a closed bounded interval is Riemann integrable.
. We also use the fact that every continuous function on a closed bounded interval is Riemann integrable.
The second fact implies that 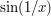 is integrable between
is integrable between 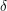 and
and  for every
for every 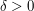 . Riemann's criterion tells us both that it is enough to find a dissection with upper and lower sums that are close and that we can find such a dissection if we just look at the interval
. Riemann's criterion tells us both that it is enough to find a dissection with upper and lower sums that are close and that we can find such a dissection if we just look at the interval ![[\delta,1]](../images/tex/76775a33874930818683098c1badb1d2.png) . But in that case, we can simply choose a dissection of
. But in that case, we can simply choose a dissection of ![[\delta,1]](../images/tex/76775a33874930818683098c1badb1d2.png) such that the upper and lower sums differ by at most
such that the upper and lower sums differ by at most 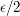 , and turn it into a dissection of
, and turn it into a dissection of ![[0,1]](../images/tex/ccfcd347d0bf65dc77afe01a3306a96b.png) by adding the interval
by adding the interval ![[0,\delta]](../images/tex/a34664f03737299494921949732f8c35.png) to the beginning. What can this extra interval
to the beginning. What can this extra interval ![[0,\delta]](../images/tex/a34664f03737299494921949732f8c35.png) contribute to the difference between the upper and lower sums? At most
contribute to the difference between the upper and lower sums? At most 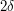 , since no two values of
, since no two values of 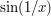 differ by more than
differ by more than 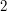 . So if we choose
. So if we choose 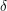 to be
to be 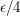 , then the complete dissection has upper and lower sums that differ by at most
, then the complete dissection has upper and lower sums that differ by at most 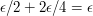 .
.
General discussion
The basic idea of the above proof was that the only point where a problem arises is 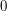 . So we contain
. So we contain 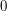 in a very small interval and don't bother to cut that interval up in a clever way: instead we simply use the fact that it is thin and not too tall. As for the rest of
in a very small interval and don't bother to cut that interval up in a clever way: instead we simply use the fact that it is thin and not too tall. As for the rest of ![[0,1]](../images/tex/ccfcd347d0bf65dc77afe01a3306a96b.png) , there we don't have any trouble because
, there we don't have any trouble because  is continuous, so we use known facts to find a good dissection of that part.
is continuous, so we use known facts to find a good dissection of that part.
Example 2
Let ![[0,1]\rightarrow\R](../images/tex/887cfc538c4cb6e6370a98c65bf01d15.png) be defined as follows. If
be defined as follows. If  is irrational, then
is irrational, then 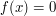 . If
. If 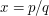 , where
, where  and
and 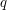 are non-negative integers with highest common factor
are non-negative integers with highest common factor  , then
, then 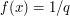 . Then
. Then  is Riemann integrable.
is Riemann integrable.
Here, we have infinitely many discontinuities (one at every rational), so our job is less easy. However, the discontinuity at 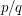 is only a jump of
is only a jump of 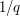 , and we can exploit this as follows. Suppose we are trying to find a dissection with upper and lower sums that differ by at most
, and we can exploit this as follows. Suppose we are trying to find a dissection with upper and lower sums that differ by at most  . First let
. First let  be a positive integer greater than
be a positive integer greater than 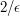 . Now if
. Now if 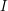 is any interval that contains no rational with denominator less than
is any interval that contains no rational with denominator less than  , then the supremum of
, then the supremum of  over all
over all 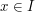 is less than
is less than 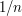 , and the infimum is
, and the infimum is 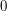 . So the contribution
. So the contribution 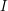 makes to the difference between the upper and lower sums of a dissection that includes
makes to the difference between the upper and lower sums of a dissection that includes 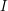 is at most
is at most 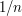 times the width of
times the width of 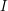 . Therefore, the total contribution from all such intervals is at most
. Therefore, the total contribution from all such intervals is at most 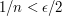 . So what do we do now? Well. there are at most
. So what do we do now? Well. there are at most 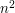 rationals in
rationals in ![[0,1]](../images/tex/ccfcd347d0bf65dc77afe01a3306a96b.png) with denominator less than
with denominator less than  . Around each one put an interval of width at most
. Around each one put an interval of width at most 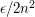 . Call these the bad intervals. Then add in some other intervals to make up a dissection of
. Call these the bad intervals. Then add in some other intervals to make up a dissection of ![[0,1]](../images/tex/ccfcd347d0bf65dc77afe01a3306a96b.png) , and call these ones the good intervals. Then the total contribution to the difference between the upper and lower sums is at most
, and call these ones the good intervals. Then the total contribution to the difference between the upper and lower sums is at most 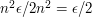 from the bad intervals and
from the bad intervals and 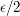 from the good intervals, so we are done.
from the good intervals, so we are done.
General discussion
In the first example, there is only one difficult point: 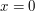 . In the second, the situation is more subtle: there are difficulties at all rationals, but they become less and less severe as the denominators increase, and there are only finitely many rationals of any given denominator.
. In the second, the situation is more subtle: there are difficulties at all rationals, but they become less and less severe as the denominators increase, and there are only finitely many rationals of any given denominator.
The method explained here is a special case of the divide and conquer trick.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)