Quick description
Many mathematical problems require one to prove that a mathematical object with certain properties exists. There are many different techniques for proving existence statements. This page briefly describes some of these and gives links to more detailed discussions. It ends with remarks on how to recognise which technique is most likely to be appropriate to any given problem. [It may well be possible to add to these, or otherwise improve them.]
General discussion
A large number of mathematical problems require one to prove that a mathematical object with certain properties exists. More ... ( Sometimes this is a very direct requirement of the problem: for example, a well-known problem (now solved) is whether there exists a polynomial in several real variables that takes only positive values but that cannot be written as a sum of squares of other polynomials. (The answer is yes.) But even more common are problems that are logically of the form "For all  there exists
there exists 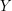 such that ***." Such a problem can be regarded as an existence problem with
such that ***." Such a problem can be regarded as an existence problem with  treated as a parameter. For instance, a well-known question in graph theory asks whether for every pair of positive integers
treated as a parameter. For instance, a well-known question in graph theory asks whether for every pair of positive integers  and
and  there exists a graph with chromatic number greater than
there exists a graph with chromatic number greater than  , which means that there is no way of colouring the vertices with
, which means that there is no way of colouring the vertices with  colours without there being an edge that joins two vertices of the same colour, and girth at least
colours without there being an edge that joins two vertices of the same colour, and girth at least  , which means that there is no cycle of length less than
, which means that there is no cycle of length less than  . Here
. Here  and
and  can be thought of as fixed (but unspecified), and the problem is then to determine whether there exists a graph with a certain property that is defined in terms of
can be thought of as fixed (but unspecified), and the problem is then to determine whether there exists a graph with a certain property that is defined in terms of  and
and  . (The answer is again yes, whatever the values of
. (The answer is again yes, whatever the values of  and
and  .)
There are many techniques for proving existence statements, and they can be strikingly different from one another. In this article we give links to articles about some of these techniques. For a quick indication of what an article is about, click on "Brief summary"). We continue with a general discussion about how to decide which of these techniques is most likely to help with the existence statement you are trying to prove. At the end of the article is a list of links to more specific articles about proving the existence of particular kinds of mathematical object. )
.)
There are many techniques for proving existence statements, and they can be strikingly different from one another. In this article we give links to articles about some of these techniques. For a quick indication of what an article is about, click on "Brief summary"). We continue with a general discussion about how to decide which of these techniques is most likely to help with the existence statement you are trying to prove. At the end of the article is a list of links to more specific articles about proving the existence of particular kinds of mathematical object. )
Technique 1: off-the-shelf examples Brief summary ( Suppose that you are asked to prove that a mathematical object  of a given kind (such as a prime number, or a group, or a function from the real numbers to the real numbers) exists with certain properties. The most obvious method is probably to look at familiar examples of that kind of mathematical object and see if one of them has the property in question. For example, does there exist a function from the reals to the reals that is non-constant, bounded, and infinitely differentiable? Most people would answer that question by having a thought such as, "Polynomials don't work, so what's the next simplest sort of function? I could try
of a given kind (such as a prime number, or a group, or a function from the real numbers to the real numbers) exists with certain properties. The most obvious method is probably to look at familiar examples of that kind of mathematical object and see if one of them has the property in question. For example, does there exist a function from the reals to the reals that is non-constant, bounded, and infinitely differentiable? Most people would answer that question by having a thought such as, "Polynomials don't work, so what's the next simplest sort of function? I could try 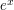 but that doesn't work either because it's unbounded. Ah, I could use
but that doesn't work either because it's unbounded. Ah, I could use 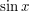 or
or 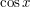 ."
It is unlikely that you will be able to solve an unsolved existence problem by simply searching around for a known example that does the job for you, unless the difficulty lies in showing that the known example has the property you want. However, not all existence problems arise directly as unsolved problems. For instance, you might be thinking about another problem and realize that it would be helpful if you could prove a certain lemma of the form "For every
."
It is unlikely that you will be able to solve an unsolved existence problem by simply searching around for a known example that does the job for you, unless the difficulty lies in showing that the known example has the property you want. However, not all existence problems arise directly as unsolved problems. For instance, you might be thinking about another problem and realize that it would be helpful if you could prove a certain lemma of the form "For every  there exists
there exists 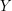 such that ..." Then you would be faced with a "mini-problem" of a kind that comes up a lot in research. You would not necessarily know in advance whether it was easy or hard, so it would be worth searching for an off-the-shelf construction of
such that ..." Then you would be faced with a "mini-problem" of a kind that comes up a lot in research. You would not necessarily know in advance whether it was easy or hard, so it would be worth searching for an off-the-shelf construction of 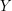 rather than starting from scratch. It also often happens that a non-trivial counterexample to one conjecture can be modified to disprove several others: it is worth getting to know the important counterexamples in your area in case you can use them for your own purposes in another context. )
rather than starting from scratch. It also often happens that a non-trivial counterexample to one conjecture can be modified to disprove several others: it is worth getting to know the important counterexamples in your area in case you can use them for your own purposes in another context. )
Technique 2: building a bespoke example Brief summary ( Another very obvious idea for proving existence statements is to design examples specifically to have the properties that are being asked for. For instance, Euclid's proof that there are infinitely many primes does this: he assumes that there are finitely many primes 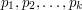 and then designs the number
and then designs the number 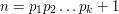 not to be a multiple of any of those primes. )
not to be a multiple of any of those primes. )
Technique 3: building complicated examples out of simple ones Brief summary ( Using mathematical processes such as products, quotients, direct sums, limits, and passing to substructures, one can often create exotic structures using more everyday ones as building blocks. )
Technique 4: making one mathematical structure out of another Brief summary ( There are many ways of building one kind of mathematical object out of another. For example, given a graph  with
with  vertices one can define an
vertices one can define an 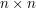 symmetric matrix
symmetric matrix 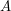 by taking
by taking 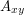 to be 1 if
to be 1 if 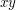 is an edge of
is an edge of  and 0 otherwise. Or given a connected manifold one can define its fundamental group. Or given a group one can define its group algebra. The list of ways in which one object can be used in the construction of another is very long. )
and 0 otherwise. Or given a connected manifold one can define its fundamental group. Or given a group one can define its group algebra. The list of ways in which one object can be used in the construction of another is very long. )
Technique 5: universal examples with given properties Brief summary ( Suppose you are asked to prove that a mathematical object  of a certain type can be found that satisfies some property
of a certain type can be found that satisfies some property 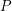 . It quite often happens that there is a partial order on the given kinds of objects such that if
. It quite often happens that there is a partial order on the given kinds of objects such that if  is less than
is less than 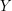 and
and  has property
has property 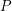 , then so does
, then so does 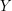 . If that is the case, then one can look for objects that are maximal in this partial order. This observation leads to the notion of a universal construction. )
. If that is the case, then one can look for objects that are maximal in this partial order. This observation leads to the notion of a universal construction. )
Technique 6: the probabilistic method Brief summary ( If you are trying to prove that an object  of type
of type  exists with certain properties, and if those properties seem to force
exists with certain properties, and if those properties seem to force  to be "spread about" and "unstructured", then a good method may well be to define a simple probability distribution on all objects of type
to be "spread about" and "unstructured", then a good method may well be to define a simple probability distribution on all objects of type  and prove that there is a non-zero probability that a randomly chosen
and prove that there is a non-zero probability that a randomly chosen  has the desired properties. )
has the desired properties. )
Technique 7: cardinality, measure and category Brief summary ( If you want to prove that there is an object  that satisfies many properties
that satisfies many properties 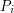 at the same time, then a good way to do so is to prove that for each
at the same time, then a good way to do so is to prove that for each 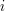 the set of objects
the set of objects  that do not satisfy
that do not satisfy 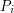 is "small" in some sense. If it can then be shown that the union of an appropriate number of small sets cannot consist of all objects
is "small" in some sense. If it can then be shown that the union of an appropriate number of small sets cannot consist of all objects  , then the proof is complete. Cardinality, measure and category all give useful notions of smallness.)
, then the proof is complete. Cardinality, measure and category all give useful notions of smallness.)
Existence proofs in more specific contexts
This article is a very general one about proving existence statements. However, there are other articles devoted to the existence of particular kinds of objects such as groups with certain properties, or graphs, or sets of integers, or normed spaces, or functions, etc. There is considerable overlap between those articles and this general one, but if you know that it is a group that you want to construct, then it may be more efficient to look at the article about existence of groups rather than this general article about existence.
Proving the existence of groups with certain properties
Proving the existence of subsets with certain properties
Proving the existence of sets of integers with certain properties
Proving the existence of finite subsets of groups with certain properties
Proving the existence of graphs with certain properties
Proving the existence of functions with certain properties
Creating real numbers using limiting arguments
How do I decide which technique to use?
It is difficult to give a definitive answer to this question, but there are certainly features to look out for when one is trying to assess which style of proof is most likely to be suitable for a given existence problem. Looking for an example amongst a list of well-known constructions is usually best if you have only just come across the problem and have no evidence to suggest how hard it is. One can think of this as a preliminary test: if you don't come across an example, then the act of establishing that well-known examples don't work may at least provide a few clues about how to go about the proof.
If off-the-shelf examples (listed as Technique 1) don't solve your problem, what should you do next? Here are some questions that can help with the decision. Suppose that your problem is of the form "Does there exist an  such that
such that 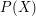 ?" Here
?" Here  is some type of mathematical object, like a field or an analytic function from
is some type of mathematical object, like a field or an analytic function from 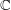 to
to 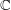 , and
, and 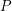 is some property that
is some property that  may or may not have. Then it can make a big difference if
may or may not have. Then it can make a big difference if 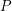 can be split up into several different properties. For example, returning to Euclid's proof that there are infinitely many primes, he assumes that the only primes are
can be split up into several different properties. For example, returning to Euclid's proof that there are infinitely many primes, he assumes that the only primes are 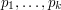 , and is faced with the question, "Does there exist
, and is faced with the question, "Does there exist  such that
such that  is not a multiple of any prime?" If it were not fairly easy to come up with an example of such an
is not a multiple of any prime?" If it were not fairly easy to come up with an example of such an  (under the hypothesis that will thereby be contradicted), then it would be possible to exploit the fact that this property splits up into the
(under the hypothesis that will thereby be contradicted), then it would be possible to exploit the fact that this property splits up into the  properties "
properties "  is not a multiple of
is not a multiple of 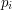 " and prove the result as one proves the Chinese remainder theorem. The idea would be to start by finding a number
" and prove the result as one proves the Chinese remainder theorem. The idea would be to start by finding a number 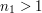 that wasn't a multiple of
that wasn't a multiple of 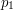 and remember that adding any multiple of
and remember that adding any multiple of 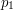 to it would give another non-multiple of
to it would give another non-multiple of 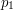 . So if
. So if 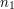 was a multiple of
was a multiple of 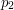 , one could add
, one could add 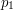 to it and the result would no longer be a multiple of
to it and the result would no longer be a multiple of 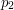 since
since 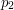 is not a factor of
is not a factor of 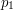 . To this new number
. To this new number 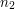 one could add any multiple of
one could add any multiple of 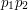 and it would still not be a multiple of either
and it would still not be a multiple of either 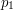 or
or 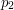 . So if
. So if 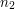 was a multiple of
was a multiple of 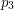 one could add
one could add 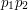 to it and the result would no longer be a multiple of
to it and the result would no longer be a multiple of 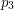 , since
, since 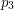 is not a factor of
is not a factor of 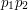 . (This is a fairly deep fact, however.) And so on all the way up to
. (This is a fairly deep fact, however.) And so on all the way up to 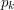 . Of course, the usual proof of just exhibiting the number
. Of course, the usual proof of just exhibiting the number 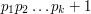 is simpler for this problem, but the fact that we can split the property up as a conjunction of several simpler properties does at least show that there is a way of solving the problem that doesn't need one to have that idea and just deals with the properties one by one. To summarize, you should ask yourself: does the property I am looking for split up as the conjunction of several simple properties?
is simpler for this problem, but the fact that we can split the property up as a conjunction of several simpler properties does at least show that there is a way of solving the problem that doesn't need one to have that idea and just deals with the properties one by one. To summarize, you should ask yourself: does the property I am looking for split up as the conjunction of several simple properties?
If the answer is yes, then there are other important questions you should ask. A very obvious one is: do I have finitely many constraints or infinitely many? And a less obvious but perhaps more important one: are the simple properties "loose constraints" on  or "tight constraints" on
or "tight constraints" on  ? And a closely related question: does
? And a closely related question: does  have many degrees of freedom or few?
have many degrees of freedom or few?
Roughly speaking, a loose constraint is one that does not cut down by too much the space of all possibilities for  . For example, if you are trying to find a sequence of integers that satisfies properties
. For example, if you are trying to find a sequence of integers that satisfies properties 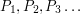 , and property
, and property 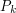 requires that every term of the sequence beyond a certain point
requires that every term of the sequence beyond a certain point 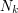 is at least as big as
is at least as big as 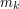 , then that is probably a loose constraint, since there is still a vast amount of flexibility in how you choose your sequence. (I say "probably" because it might conceivably be that in the presence of the other properties that the sequence is required to have, this property does hugely cut down the possibilities. But it is usually quite easy to recognise a loose constraint when you have one.) Having loose constraints is helpful if the object
, then that is probably a loose constraint, since there is still a vast amount of flexibility in how you choose your sequence. (I say "probably" because it might conceivably be that in the presence of the other properties that the sequence is required to have, this property does hugely cut down the possibilities. But it is usually quite easy to recognise a loose constraint when you have one.) Having loose constraints is helpful if the object  that you want to exist can be built up in stages. In the case of a sequence, it is obvious that this can be done: one builds up the sequence an element at a time. But it also applies to less clearly composite objects such as real numbers, which can be defined as limits of sequences. And as the discussion of Euclid's proof showed, even a positive integer can on occasion be built up in stages.
that you want to exist can be built up in stages. In the case of a sequence, it is obvious that this can be done: one builds up the sequence an element at a time. But it also applies to less clearly composite objects such as real numbers, which can be defined as limits of sequences. And as the discussion of Euclid's proof showed, even a positive integer can on occasion be built up in stages.
Sometimes one can prove that there is an object  with many properties
with many properties 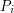 by proving that for every
by proving that for every 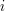 the set
the set 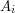 of objects that do not have property
of objects that do not have property 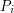 is small. If the sets
is small. If the sets 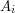 are small enough in a suitable sense (that varies from problem to problem) then one may be able to show that their union cannot include all objects
are small enough in a suitable sense (that varies from problem to problem) then one may be able to show that their union cannot include all objects  . If objects of type
. If objects of type  have finitely many degrees of freedom and one wants to find
have finitely many degrees of freedom and one wants to find  with finitely many properties
with finitely many properties 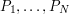 , then one may be able to assign sizes to each set of objects without property
, then one may be able to assign sizes to each set of objects without property 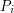 and show that these sizes add up to less than the size of the set of all objects of type
and show that these sizes add up to less than the size of the set of all objects of type  . This is how the probabilistic method (Technique 7) works. If there is a countably infinite collection of properties, then one often tries to find a notion of smallness with the following two features: a countable union of small sets is small; the set of all objects of type
. This is how the probabilistic method (Technique 7) works. If there is a countably infinite collection of properties, then one often tries to find a notion of smallness with the following two features: a countable union of small sets is small; the set of all objects of type  is not small. Then if the set
is not small. Then if the set 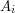 of all objects of type
of all objects of type  without property
without property 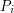 is small for each
is small for each 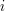 , it follows that there is some
, it follows that there is some  that has all the properties
that has all the properties 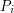 . Some common notions of smallness are being countable, having measure zero, and being of the first category. Proofs of this kind are explained in the article cardinality, measure and category listed as Technique 7 above. These techniques are a very good way of reversing quantifiers to obtain uniform statements: you are trying to prove the uniform statement that there exists a single
. Some common notions of smallness are being countable, having measure zero, and being of the first category. Proofs of this kind are explained in the article cardinality, measure and category listed as Technique 7 above. These techniques are a very good way of reversing quantifiers to obtain uniform statements: you are trying to prove the uniform statement that there exists a single  such that
such that 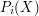 holds for every
holds for every 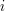 ; what you can prove easily is that for each
; what you can prove easily is that for each 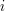 there is an
there is an 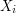 such that
such that 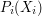 holds; but you manage to show that, for every
holds; but you manage to show that, for every 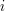 , all but a small set of
, all but a small set of  satisfies
satisfies 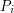 and that is enough to show that some
and that is enough to show that some  satisfies every
satisfies every 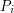 . This type of problem is discussed in more detail in the article entitled How to change "for all x there exists y" into "there exists y such that for all x".
. This type of problem is discussed in more detail in the article entitled How to change "for all x there exists y" into "there exists y such that for all x".
Actually, there are two ways of using the probabilistic method. One was described above: one would like properties 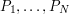 to hold, one chooses a random
to hold, one chooses a random  , one shows that for each
, one shows that for each 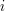 the probability that
the probability that  does not have property
does not have property 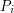 is at most
is at most 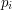 , and one shows that
, and one shows that 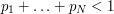 . But if the probabilities add up to more than 1, it may still be possible to prove that an
. But if the probabilities add up to more than 1, it may still be possible to prove that an  exists with all the properties
exists with all the properties 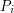 if they are sufficiently independent. To give a silly example, let the objects in question be outcomes when a die is thrown
if they are sufficiently independent. To give a silly example, let the objects in question be outcomes when a die is thrown  times: that is, each
times: that is, each  is a sequence like
is a sequence like 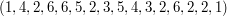 . Let
. Let  be the property "no six is thrown". This splits up as a conjunction of the properties
be the property "no six is thrown". This splits up as a conjunction of the properties  , where
, where 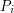 is the property "the
is the property "the 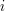 th throw is not a six". The probability that
th throw is not a six". The probability that  fails to have property
fails to have property 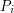 is
is 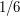 , so if
, so if 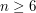 we cannot argue that the failure probabilities add up to less than 1. However, the properties are independent, so we can say that the probability that
we cannot argue that the failure probabilities add up to less than 1. However, the properties are independent, so we can say that the probability that  has the required property is
has the required property is 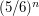 , which is greater than 0.
, which is greater than 0.
One can think of the Euclid proof in this way too: 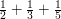 is greater than 1, but we can still find a number that is not a multiple of
is greater than 1, but we can still find a number that is not a multiple of 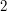 ,
, 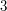 or
or 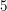 because the properties "
because the properties "  is not a multiple of the prime
is not a multiple of the prime 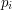 " are independent in a suitable sense.
" are independent in a suitable sense.
The main reason for mentioning this is that a somewhat similar distinction operates with infinitary proofs as well. Sometimes one tries to prove that each set 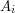 of
of  that fail property
that fail property 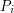 is small. But sometimes there is no obvious way of doing this, and instead one tries to prove that for each
is small. But sometimes there is no obvious way of doing this, and instead one tries to prove that for each  the set
the set 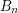 of
of  that satisfies properties
that satisfies properties 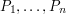 has a structure that is still flexible enough to make it possible to find inside it an
has a structure that is still flexible enough to make it possible to find inside it an  that satisfies
that satisfies 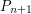 as well. (And then one needs some kind of limiting argument to show that the intersection of all the
as well. (And then one needs some kind of limiting argument to show that the intersection of all the 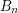 is non-empty.) In the first case, the reason the constraints are "loose" is just that they don't rule out many
is non-empty.) In the first case, the reason the constraints are "loose" is just that they don't rule out many  , whereas in the second case the looseness is somehow more structural: they knock out a few degrees of freedom but leave you with many more to play with.
, whereas in the second case the looseness is somehow more structural: they knock out a few degrees of freedom but leave you with many more to play with.
The techniques discussed so far are more likely to be appropriate for analysis, set theory and combinatorics, where problems with loose constraints arise more often than they do in algebra, geometry and number theory, say. There it is much more likely that the right techniques will be a mixture of using off-the-shelf examples (Technique 1), building complicated examples out of simple ones (Technique 3), making one mathematical structure out of another (Technique 4), and, under special circumstances (explained in the brief summary above) universal constructions (Technique 5).
We thus have two extremes. On one side we have problems where we are typically dealing with objects with many degrees of freedom, which lend themselves to being built up in stages, and we face constraints that for one reason or another do not interfere with each other too much. On the other side, there are objects that are highly structured, so that a few decisions can determine the object in its entirety, and we face constraints that seem to interfere with each other so much that it will take a miracle (which we hope eventually to see is not a miracle) for them to be compatible.
There is also a fascinating area in between, where we have a certain amount of flexibility to build an object up, but also a certain amount of rigidity that stops us being able to use techniques such as just-do-it proofs (an example of Technique 2) or the probabilistic method (Technique 7) or notions of smallness (Technique 8). Here are three examples.
1. A well-known open problem in combinatorics is to decide whether the following bipartite graph contains a Hamilton cycle: its vertices are subsets of 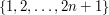 , and we join a set
, and we join a set 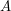 to a set
to a set 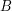 if
if 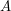 is a proper subset of
is a proper subset of 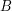 or vice versa. If you try to build up such a path, then you find that it is easy to start with but becomes difficult when you've been going for a while. But there is so much flexibility in the early stages that it is hard to see any helpful structures jumping out.
or vice versa. If you try to build up such a path, then you find that it is easy to start with but becomes difficult when you've been going for a while. But there is so much flexibility in the early stages that it is hard to see any helpful structures jumping out.
2. Another well-known problem is whether there are 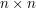 Hadamard matrices for every
Hadamard matrices for every  that is a multiple of 4. These are
that is a multiple of 4. These are 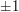 -valued matrices for which the rows are orthogonal. For example,
-valued matrices for which the rows are orthogonal. For example, 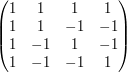 is a Hadamard matrix. Here again it is reasonably easy to build up such a matrix for a while, but then the going gets tough. There are a number of clever constructions of classes of such matrices but they do not give examples for every multiple of 4.
is a Hadamard matrix. Here again it is reasonably easy to build up such a matrix for a while, but then the going gets tough. There are a number of clever constructions of classes of such matrices but they do not give examples for every multiple of 4.
3. A nice problem in complex analysis (this one solved) is the following question. If 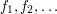 are holomorphic functions on the disc that converge pointwise to a function
are holomorphic functions on the disc that converge pointwise to a function  , then must
, then must  be holomorphic? The difficulty here is that holomorphic functions have a lot of rigidity, which makes it difficult to construct a counterexample, and also a lot of flexibility, which makes it difficult to prove a theorem. In fact, there is a sense in which holomorphic functions are exactly half way between completely flexible and completely rigid: they are given by power series of the form
be holomorphic? The difficulty here is that holomorphic functions have a lot of rigidity, which makes it difficult to construct a counterexample, and also a lot of flexibility, which makes it difficult to prove a theorem. In fact, there is a sense in which holomorphic functions are exactly half way between completely flexible and completely rigid: they are given by power series of the form 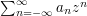 , where "half of the coefficients" (the ones for negative
, where "half of the coefficients" (the ones for negative  ) are zero.
) are zero.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)