Quick description
This page gives a summary of several techniques that are commonly used for answering questions of the form, ``Does there exist a group  such that ...?'' The emphasis is on discrete groups. There is another article with a discussion of topological groups and Lie groups.
such that ...?'' The emphasis is on discrete groups. There is another article with a discussion of topological groups and Lie groups.
Prerequisites
A basic knowledge of group theory, such as would be taught in typical first course on the subject.
 |
Method 1: Check the desired conditions against a library of well-known examples
The most obvious way of determining whether a group exists with a certain property is to look at the groups you know and see whether it has the property in question. Here is a list of well-known groups, with brief discussions of the kinds of properties they can be expected to have. And here is a list of some important group properties, including several examples of which groups have each possible set of properties.
Another approach is to rely on group libraries in a computer algebra package such as GAP. It is often possible to define the property in question in GAP notation and quickly scan large sets of groups to see if any of them has this property.
There is also a more general page about off-the-shelf examples in mathematics.
Method 2: Write down a presentation.
An important way of specifying a group is by means of generators and relations. For instance, the dihedral group of order 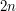 is the group with two generators
is the group with two generators  and
and 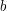 subject to the relations
subject to the relations 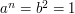 (where
(where  is the identity of the group) and
is the identity of the group) and 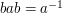 . (It can also be defined as the group of symmetries of a regular n-gon.) For more details, see this article about presentations of groups.
. (It can also be defined as the group of symmetries of a regular n-gon.) For more details, see this article about presentations of groups.
Method 3: Take interesting subgroups of existing groups.
Some groups are conveniently described as subgroups of larger groups.
Method 4: Build new groups out of old ones using products and quotients.
There are several different kinds of products, described here. As well as descriptions of the products themselves are descriptions of the kinds of uses to which they are typically put. Quotients are described here.
Method 5: Take the group of symmetries of some other mathematical object.
This method could be regarded as a special case of Method 1, but it is sufficiently important to deserve a space of its own.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)