 |
Quick description
This article is about how to prove that a function is Riemann integrable if for some reason you need to do so directly from the definition.
Prerequisites
Basic undergraduate real analysis.
Example 1
If  and
and 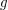 are both Riemann integrable functions defined on
are both Riemann integrable functions defined on ![[a,b]](../images/tex/2c3d331bc98b44e71cb2aae9edadca7e.png) , then so is
, then so is 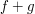 , and
, and 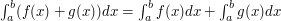 .
.
Example 2
Every monotone function defined on the closed interval ![[a,b]](../images/tex/2c3d331bc98b44e71cb2aae9edadca7e.png) is Riemann integrable.
is Riemann integrable.
Example 3
Every continuous function on the closed interval ![[a,b]](../images/tex/2c3d331bc98b44e71cb2aae9edadca7e.png) is Riemann integrable.
is Riemann integrable.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)