Quick description
In analysis and analytic number theory, one sometimes obtains estimates for expressions involving several variables or parameters subject to various constraints concerning their respective sizes. If these estimates have to be carried along and transformed in substantial ways, or if many of them involving different constraints must be combined at some point, it may be useful (if it is possible) to incorporate the constraints inside the estimates by adding terms which make the estimate trivial if the constraints are not satisfied, and reduce to the useful estimate otherwise.
This is similar in spirit to the use of a characteristic function of a set to represent a summation or integration condition, as described in Getting rid of nasty cutoffs for example.
Prerequisites
Basic calculus or even simple combinatorics and sums.
General discussion
The idea of the trick is best explained with concrete elementary examples.
Example 1
Consider the inequality
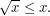
This is only valid if 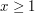 . However, if we write
. However, if we write
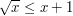
the inequality is valid for 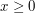 , and is not asymptotically worse than the previous one when
, and is not asymptotically worse than the previous one when  gets large.
gets large.
Example 2
Suppose you have a function 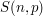 depending on an integer
depending on an integer 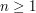 and a prime number
and a prime number  , and that you know the upper bound
, and that you know the upper bound
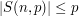
for all  , and
, and
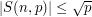
if  does not divide
does not divide  . If these estimates are used extensively later on, with different values of
. If these estimates are used extensively later on, with different values of  and
and  , sorting out which of the two applies may become a bookkeeping nightmare. Writing
, sorting out which of the two applies may become a bookkeeping nightmare. Writing
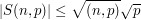
where 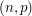 is the GCD of
is the GCD of  and
and  encapsulates both statements neatly and is much easier to carry around and combine with other estimates.
encapsulates both statements neatly and is much easier to carry around and combine with other estimates.
 |
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)