Quick description
This article describes situations where one can use multiplication to compute the number of elements of a set of vectors or strings.
Prerequisites
Basic mathematical notation.
General discussion
We start with the following elementary fact:
if 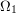 ,
, 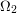 ,...,
,..., 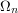 are finite sets and
are finite sets and 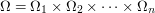 then
then
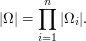
The truth of this statement follows from the definition of multiplication for positive integers and induction.
Number of elements in cartesian products where the 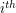 set depends on the first
set depends on the first 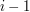 components
components
In many situations we are interested in a set 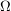 whose elements
are strings (or vectors) of length
whose elements
are strings (or vectors) of length  such that the set where
the
such that the set where
the 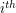 component takes values depends on the values of the previous
component takes values depends on the values of the previous
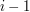 components of the string. Then one can write
components of the string. Then one can write 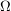 as follows:
as follows:
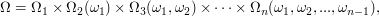
where an element of 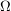 is denoted with
is denoted with 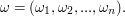
If
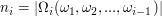
is independent of 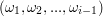 then
then
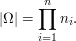
Example 1
Several basic counting formulas follow from this principle.
For example, the number of permutations of length  from a finite set
from a finite set 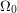 is
is
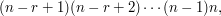
where 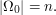
Example 2
In the previous example 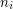 is a decreasing sequence.
Here is an example where
is a decreasing sequence.
Here is an example where 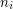 is increasing (Feller, Probability Theory, Vol I, Third Edition). Suppose there are
is increasing (Feller, Probability Theory, Vol I, Third Edition). Suppose there are  flag poles and each pole
can contain arbitrary number of flags. What are the number of possible
ways to put
flag poles and each pole
can contain arbitrary number of flags. What are the number of possible
ways to put  distinct flags on these
distinct flags on these  poles if the order of the flags
on the poles is important? In this example
poles if the order of the flags
on the poles is important? In this example 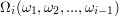 is the possible places where the
is the possible places where the 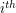 flag can be put.
flag can be put. 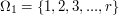 , i.e., for the first flag we simply pick a pole. Let
, i.e., for the first flag we simply pick a pole. Let 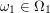 denote the pole where the first flag is put. Then
denote the pole where the first flag is put. Then
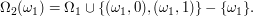
where 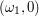 refers to the position before the first flag on the poll where this flag is and
refers to the position before the first flag on the poll where this flag is and 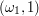 refers to the position after. It follows that
refers to the position after. It follows that
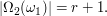
Let 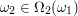 denote the position of the second flag. Then the set of all possible positions for the third
flag are:
denote the position of the second flag. Then the set of all possible positions for the third
flag are:
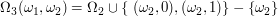
and it follows that
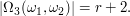
In general for the 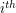 flag the set of all possible positions are
flag the set of all possible positions are
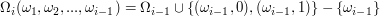
and
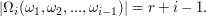
It is clear that the problem is in the range of our method and we have
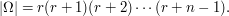
Example 3
Here is an example where the idea does not apply.
Let 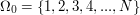 . Let
. Let 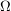 be the set
of ordered strings from the alphabet
be the set
of ordered strings from the alphabet 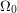 of length
of length  .
. 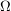 has the same
structure as the one given in the display above with
has the same
structure as the one given in the display above with
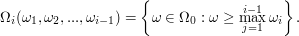
Clearly, here 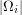 is a function of
is a function of 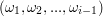 and we cannot obtain
and we cannot obtain 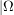 as simple multiplication.
However, this problem can be embedded in a counting problem that yields to multiplication,
see Example 2 in the article on counting and partitioning.
as simple multiplication.
However, this problem can be embedded in a counting problem that yields to multiplication,
see Example 2 in the article on counting and partitioning.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)