 |
Quick description
In order to evaluate some mathematical expression it is often benefitial to combine terms with a common property.
Prerequisites
Some real analysis.
Example 1
If one has the Riemann zeta function
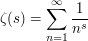
then the sum is absolutely convergent for Re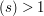 .
.
Therefore it can be rearranged in every possible manner. Now let
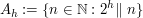
where 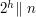 means that
means that 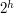 divides
divides  but
but 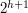 does not.
Then the set
does not.
Then the set 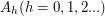 form a partition of
form a partition of 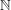 and we get
and we get
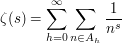
But now we can write 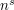 as
as 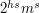 where
where
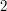 does not divide
does not divide 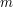 and we get
and we get
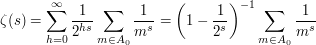
by the geometric sum formula.
Applying this to all the other primes 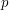 and using a limiting argument we establish
the product formula
and using a limiting argument we establish
the product formula

 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)