Suppose that you are trying to prove by induction that the statement 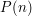holds for every positive integer , and suppose that you are having difficulties deducing 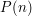from 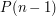. One option you have is to work on a different statement 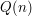. If 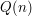implies 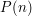and if 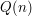can be proved by induction, then you have proved 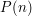. This often turns out to be a very helpful technique.