Tricki
a repository of mathematical know-how

The van der Corput lemma for equidistribution

Stub iconThis article is a stub.This means that it cannot be considered to contain or lead to any mathematically interesting information.

Quick description

If 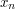x_n is a sequence mod 1, such that 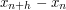x_{n+h} - x_n is uniformly distributed modulo 1 for all non-zero h, then 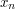x_n is also uniformly distributed modulo 1.

Prerequisites

Undergraduate analysis

Example 1

(Equidistribution of polynomials)

Example 2

(Multiple recurrence in weakly mixing systems)

General discussion

A quantitative version of this fact, known as van der Corput's inequality, is also useful.

(Also mention Bergelson's Hilbert space version.)

Not to be confused with the van der Corput lemma for oscillatory integrals.

Comments

Post new comment

(Note: commenting is not possible on this snapshot.)

Before posting from this form, please consider whether it would be more appropriate to make an inline comment using the Turn commenting on link near the bottom of the window. (Simply click the link, move the cursor over the article, and click on the piece of text on which you want to comment.)

snapshot
Notifications