Square and rearrange | Tricki

a repository of mathematical know-how

Square and rearrange

This article is incomplete. This article needs more work

Quick description

To control an integral 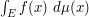$\int_E f(x)\ d\mu(x)$ or a sum 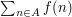$\sum_{n \in A} f(n)$ , take its magnitude squared, expand it into a double integral 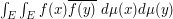$\int_E \int_E f(x) \overline{f(y)}\ d\mu(x) d\mu(y)$ or a double sum 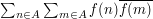$\sum_{n \in A} \sum_{m \in A} f(n) \overline{f(m)}$ , and then rearrange, for instance by making the change of variables 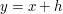$y=x+h$ or $n=m+h$ .

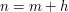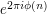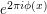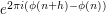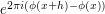This often has the effect of replacing a phase $e^{2\pi i \phi(n)}$ or $e^{2\pi i \phi(x)}$ in the original integrand by a "differentiated" phase such as $e^{2\pi i (\phi(n+h)-\phi(n))}$ or $e^{2\pi i (\phi(x+h)-\phi(x))}$ . Such differentiated phases are often more tractable to work with, especially if 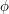$\phi$ had a "polynomial" nature to it.

Prerequisites

harmonic analysis, analytic number theory

Example 1

This is a classic example: to compute the integral 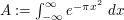$= \int_{-\infty}^\infty e^{-\pi x^2}\ dx$ , square it to obtain

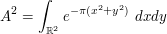
$A^2 = \int_{\R^2} e^{-\pi(x^2+y^2)}\ dx dy$

then rearrange using polar coordinates to obtain

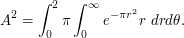
$A^2 = \int_0^2\pi \int_0^\infty e^{-\pi r^2} r\ dr d\theta.$

The right-hand side can easily be evaluated to be 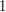$1$ , so the positive quantity 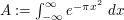$= \int_{-\infty}^\infty e^{-\pi x^2}\ dx$ must also be $1$ .

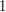Example 2

(Gauss sums)

Example 3

(Weyl sums)

Example 4

(The 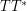$TT^*$ method, say to obtain Hormander's 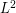$L^2$ oscillatory integral estimate)

Example 5

(The large sieve)

General discussion

A variant of this trick is the van der Corput lemma for equidistribution.

6030 reads
Subscribe

Comments

Post new comment

(Note: commenting is not possible on this snapshot.)