To calculate an infinite sum exactly, try antidifferencing

Quick description

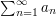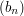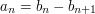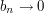If you are trying to calculate the sum $\sum_{n=1}^\infty a_n$ , then sometimes it is possible to spot another sequence $(b_n)$ such that $a_n=b_n-b_{n+1}$ and $b_n\rightarrow 0$ . If that is the case, then your sum is equal to $b_1$ .

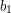Prerequisites

The definition of an infinite sum.

This article could use additional contributions. Probably there is more to be said on this theme

Example 1

An infinite sum that is well known to be straightforward to calculate exactly is the sum

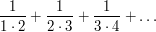
$\frac 1{1\cdot 2}+\frac 1{2\cdot 3}+\frac 1{3\cdot 4}+\dots$

The usual technique for summing this is to observe that 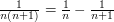$\frac 1{n(n+1)}=\frac 1n-\frac 1{n+1}$ , from which it follows that

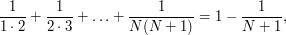
$\frac 1{1\cdot 2}+\frac 1{2\cdot 3}+\dots+\frac 1{N(N+1)}=1-\frac 1{N+1},$

which tends to 1 as 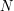$N$ tends to infinity.

This points to a circumstance in which an infinite sum can be evaluated exactly: we can work out the discrete analogue of an "antiderivative": that is, we have a sequence 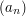$(a_n)$ and can spot a nice sequence 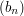$(b_n)$ such that 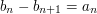$b_n-b_{n+1}=a_n$ . Of course, 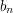$b_n$ must in that case be the partial sum 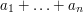$a_1+\dots+a_n$ (up to an additive constant). So is this really making the more or less tautologous observation that if you have a nice formula for the partial sums and can see easily what they converge to then you are done?

It isn't quite, because we could have spotted that 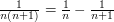$\frac 1{n(n+1)}=\frac 1n-\frac 1{n+1}$ without working out any partial sums.

General discussion

Let us try to understand better why the above trick is not a universal method for calculating all infinite sums, by contrasting the above example with the example of the sum

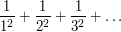
$\frac 1{1^2}+\frac 1{2^2}+\frac 1{3^2}+\dots$

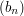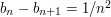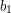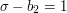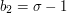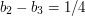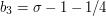Can we find some sequence $(b_n)$ such that $b_n-b_{n+1}=1/n^2$ ? It seems difficult just to spot such a sequence, so instead let us try to be systematic about it. It's not quite clear how to pick $b_1$ , so let us set it to be $\sigma$ . Then $\sigma-b_2=1$ , so $b_2=\sigma-1$ . Next, $b_2-b_3=1/4$ , so $b_3=\sigma-1-1/4$ . In general, we find that 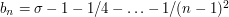$b_n=\sigma-1-1/4-\dots-1/(n-1)^2$ . 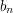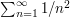Since we also want $b_n$ to tend to zero, this tells us what $\sigma$ must be: $\sum_{n=1}^\infty 1/n^2$ , precisely the sum we were trying to calculate!

The reason the technique worked in the example above was that the partial sums turned out to have a nice formula.

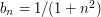Remark A simple method of generating undergraduate mathematics exercises is to reverse the telescoping-sums idea in order to create infinite sums that can be evaluated exactly. For example, take the sequence $b_n=1/(1+n^2)$ . This tends to $0$ as $n$ tends to infinity. Now let

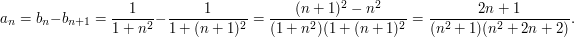
$a_n=b_n-b_{n+1}=\frac 1{1+n^2}-\frac 1{1+(n+1)^2}=\frac{(n+1)^2-n^2}{(1+n^2)(1+(n+1)^2}=\frac{2n+1}{(n^2+1)(n^2+2n+2)}.$

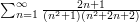The question you then ask is to calculate the sum $\sum_{n=1}^\infty\frac{2n+1}{(n^2+1)(n^2+2n+2)}$ . A smart student will use partial fractions to discover that this is a telescoping sum and will end up with the answer $b_1=1/2$ .

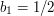If this method works, it is a bit like managing to calculate an integral by antidifferentiating the integrand.