 |
Quick description
Suppose that 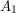 ,
, 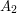 , ...,
, ..., 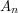 are events and you want to calculate the probability that exactly
are events and you want to calculate the probability that exactly  of these events occur. That is, you would like to compute the probability
of these events occur. That is, you would like to compute the probability ![p_{[m]}](../images/tex/5d9814ffe0a367c952fce76a7a2d3ca3.png) of the set of samples that belong to exactly
of the set of samples that belong to exactly  of these sets. One can use the following generalized inclusion-exclusion formula to accomplish this:
of these sets. One can use the following generalized inclusion-exclusion formula to accomplish this:
![p_{[m]}= \sum_{k=0}^{N-m} (-1)^{k} \binom{ m+ k}{m} \sum_{1\le i_1 < i_2 < \cdots < i_{m+k} \le n } P\left( \cap_{j=1}^{m+k} A_{i_j}\right)](../images/tex/40ce38479eb0d6d02fbda99c0ff0352b.png)
The formula looks complicated, but if the intersection probabilities 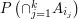 are simple to compute it gives a simple method to compute the desired probability. It can be useful in problems where it is not easy to use recursion or other techniques and when
are simple to compute it gives a simple method to compute the desired probability. It can be useful in problems where it is not easy to use recursion or other techniques and when 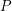 has a complex dependence structure. In its limitations and usefulness it is similar to the
ordinary inclusion exclusion principle.
has a complex dependence structure. In its limitations and usefulness it is similar to the
ordinary inclusion exclusion principle.
Prerequisites
Elementary probability.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)