Quick description
To prove that a sequence converges, it is sometimes easier to start by finding a subsequence that converges (or proving that such a subsequence exists). Then one can hope to deduce that the sequence itself converges. Another way of using subsequences is to exploit the following result: if every subsequence has a further subsequence that converges to a limit 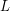 , then the whole sequence converges to
, then the whole sequence converges to 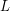 .
.
Prerequisites
Basic concepts of real analysis.
 |
Example 1
To prove that a Cauchy sequence 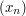 of real numbers converges, assuming one of the other forms of the completeness axiom, one can argue as follows. First, one proves the Bolzano-Weierstrass theorem. Then one observes that a Cauchy sequence is bounded, and so by the Bolzano-Weierstrass theorem has a convergent subsequence. And finally, one proves that if a Cauchy sequence has a subsequence that tends to a limit
of real numbers converges, assuming one of the other forms of the completeness axiom, one can argue as follows. First, one proves the Bolzano-Weierstrass theorem. Then one observes that a Cauchy sequence is bounded, and so by the Bolzano-Weierstrass theorem has a convergent subsequence. And finally, one proves that if a Cauchy sequence has a subsequence that tends to a limit 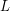 , then the sequence itself tends to
, then the sequence itself tends to 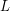 .
.
Example 2
Here is a second way of proving that Cauchy sequences converge. Let 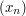 be a Cauchy sequence. By the Cauchy condition we can choose a subsequence
be a Cauchy sequence. By the Cauchy condition we can choose a subsequence 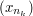 such that
such that 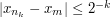 whenever
whenever 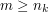 . It follows that the closed intervals
. It follows that the closed intervals ![[x_{n_k}-2\cdot 2^{-k},x_{n_k}+2\cdot 2^{-k}]](../images/tex/ca33cf03a40867d5c5b5f4c451cdc8be.png) are nested, since if
are nested, since if 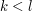 then
then ![x_{n_l}\in[x_{n_k}-2^{-k},x_{n_k}+2^{-k}]](../images/tex/97c16b8fb116eaa7d6934db3d505e29e.png) , and
, and 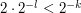 . Therefore, their intersection is non-empty. Since their lengths tend to zero, the intersection is a singleton
. Therefore, their intersection is non-empty. Since their lengths tend to zero, the intersection is a singleton 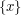 , and it is easy to check that the subsequence
, and it is easy to check that the subsequence 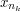 converges to
converges to  . Therefore, since
. Therefore, since 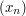 is Cauchy, so does the whole sequence.
is Cauchy, so does the whole sequence.
General discussion
The trick in the second approach was to replace a Cauchy sequence by a subsequence that was rapidly Cauchy. That gave us the inequality 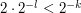 , which was crucial to the success of the proof.
, which was crucial to the success of the proof.
 Tricki
Tricki
Comments
Post new comment
(Note: commenting is not possible on this snapshot.)